Назначение

Мультимедийный комплекс "Kvartika-2.0" (грант РФФИ 05-07-90144-в) предназначен для представления структуры, условий возникновения и трансформации атомных и нанообъектов [1-5] в процессе их исследования и позволяет оперативно получать графическую дву- и трехмерную, текстовую и числовую информацию. Алгоритмы отображения атомных структур предусматривают построение бесконечномерных стохастических матриц, реализующие принципы квантовых измерений фон Неймана [6], и учитывают новые формулировки теории И.Пригожина, согласно которым основной характеристикой квантовых объектов служит не волновая функция, соответствующая амплитуде вероятности, а сама вероятность [7].

Моделирование атомных структур и свойств наноэлементов, используемые в мультимедийном комплексе [8] основываются на свойствах числовых квантовых последовательностей, которые могут быть представлены в виде квантовых степенных шкал с использованием фигурных чисел, представляющих собой результаты квантовых измерений [9].

Введение четырех логических состояний в динамический процесс измерений обусловлено вероятностями ошибок первого и второго рода, отличными от нуля и характеризующими условия проведения измерений (условия окружающей среды). Этот процесс порождает бесконечномерную матрицу квантовых измерений и позволяет каждый элемент матрицы рассматривать как результат измерения. При этом элементам матрицы удается поставить в соответствие, во-первых, определенные вероятности, взаимосвязанные с золотыми пропорциями, а, во-вторых, геометрические образы в виде фигурных чисел [9-11].

В мультимедийном комплексе предусмотрено числовое и графическое представление 75 стохастических матриц (по 75 строк и столбцов в каждой), взаимосвязанных с фигурными числами. Размещение по заданному алгоритму элементов, характеризуемых порядковыми номерами (до элемента с порядковым номером 110, включительно), в трехмерной матрице (75х75х75), позволяет сопоставить этим элементам определенный набор структурированных объектов в виде фигурных чисел [9-11].

В интерактивном режиме в программе заполняются таблицы, котрые содержат оригинальные данные об элементах, а также справочные сведения. Предусмотрена возможность пополнения таблиц (до 200 характеристик исследуемых объектов в каждой), а также передачи сводных данных таблиц в формате Excel для последующей обработки.

Программа "Kvartika-2.0" содержит в себе шесть основных разделов:

1. Матрица;
2. Грфика;
3. Структура;
4. Элемент;
5. Выборка ;
6. Система элементов

и двадцать подпрограмм (см. "Краткое описание" ).

1. Вид матрицы квантовых измерений, соответствующей золотой пропорции порядка М=1, показан на рис.1. Отметим, что о бобщенные золотые пропорции, применяемые в современном естествознании, представляют собой математические объекты, отображающие единство непрерывных и дискретных объектов на основе фрактальной симметрии [3] . В мультимедийном комплексе использованы готовые табличные данные, описывающие структуру и свойства атомных объектов, поэтому обращение к исходным данным на современных компьютерах происходит практически мгновенно, т.к. исключена необходимость проведения трудоемких длительных расчетов для элементов с порядковыми номерами до 110 включительно.

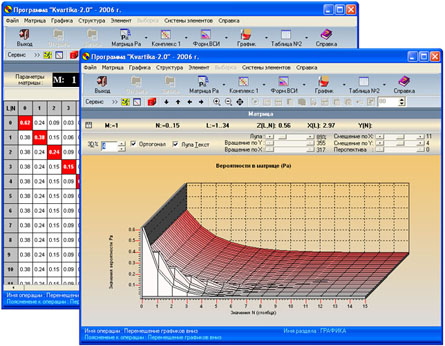
Рис.1. Представление матрицы квантовых измерений при М=1.

Элемент с порядковым номером Z в соответствии со значениями квантовых чисел для водородоподобного атома можно отобразить в матрице квантовых измерений с помощью самоподобных структур. В этом случае классификация элементов в зависимости от значений параметра М будет строго соответствовать правилам насыщения энергетических уровней водородоподобных атомов. При этом порядковому номеру Z может соответствовать несколько положений в матрице, для каждого из которых выполняется соотношение Z = N +К M и соответствующие этим положениям геометрические образы в виде фигурных чисел. Данное условие означает равенство вероятностей

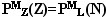
и показывает, что параметр порядка М является инвариантом отображения в матрице квантовых измерений. Здесь L , N – номера строки и столбца матрицы, величина К=1, если N < L ; К= N - L , если N >= L .

Геометрические образы элементов (в виде фигурных чисел или графов), соответствующие параметрам положения элемента с данным порядковым номером, удобно характеризовать параметрами структуры, т.е. величинами, взаимосвязанными с характеристикой Эйлера: количеством конструкций графа С , вершин графа В , ребер графа Р , односвязных плоских областей (граней) Г . Значения этих характеристик указываются в таблицах, формируемых в программной системе и показанных на рис.2.

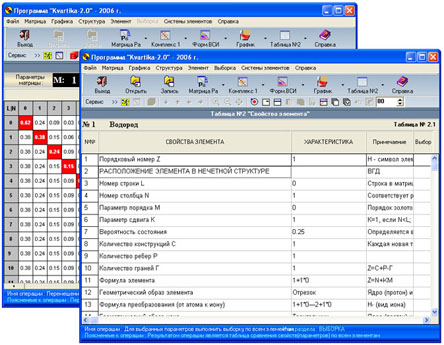
Рис.2. Формирование таблиц со свойствами элементов.

Указанные величины для любого образа элемента связаны с порядковым номером Z следующим соотношением: Z = C + P - Г . Здесь Z = B -1, так как образ элемента включает ядро и Z частиц (электронов). В частном случае выпуклых многогранников параметр С =1 и приходим к общеизвестному соотношению В + Г - Р = 2 .

Пример определения структуры элемента в зависимости от его положения в матрице, согласно данным (рис.2) показан на рис.3. Рассмотрение самоподобных множеств элементов, характеризуемых определенными порядковыми номерами, позволяет каждому элементу поставить в соответствие от одного до трех геометрический образов в виде фигурных чисел определенной размерности. Отметим, что неоднозначность в определении атомной структуры, соответствующая представлениям о полиморфизме атомных структур, была обнаружена экспериментально в начале прошлого века в опытах Майера, рассмотренных в [13] . Фигурные числа представляют собой результаты квантовых измерений и являются собственными функциями оператора конечной разности. То есть при N >= L выполнены соотношения.

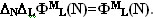
Фигурные числа определяют структуру квантовых числовых последовательностей, обладают комбинаторными и геометрическими свойствами и поэтому служат удобным инструментом для анализа атомных и наноструктур. Критерием изменчивости сложных нелинейных систем, как показано в [3], служит порядок золотой пропорции. Этот же параметр М характеризует условия окружающей среды [9-11].

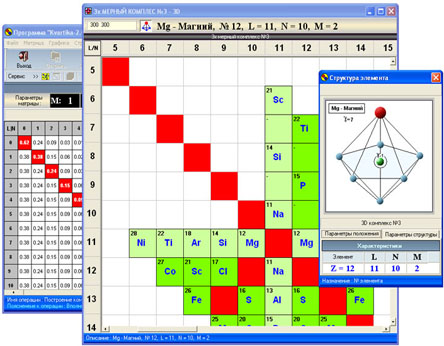
Рис.3. Представление структуры элементов в матрице.

Первая электронная оболочка моделируется крестообразной структурой (по два положения для элементов с первым и вторым порядковыми номерами). При этом сумма вероятностей четырех состояний двух элементов равна единице при М=1 (рис.3). Последующие построения моделей электронных оболочек основаны на принципе подобия. Отображение элементов, характеризуемых порядковыми номерами, в матрицу квантовых измерений можно сравнить с методом многомерного шкалирования [14]. Цель многомерного шкалирования — выявление структуры исследуемого множества элементов. Под выявлением структуры понимают выделение набора основных факторов, по которым различаются элементы, и описание элементов с помощью данных факторов. Таким образом, решаются две задачи: во-первых, определяются факторы (от одного до трех значений параметра М), влияющие на процесс измерения и приводящие к образованию определенных структур; во-вторых на основе данных измерений выявляется объективная структура системы элементов и проводится классификация элементов.