| |
Подпрограмма
"Формула В.С.Ивановой - опция "Диагонали".
В разделе "Структура"
имеется подменю, в котором
пользователь может построить ряд
относительных размеров наночастиц
по формуле В.С.Ивановой на основе
диагоналей или столбцов матрицы.
Аналогичные операции пользователь
может провести используя кнопку-меню
"Форм.ВСИ". Нажатие
данной кнопки выкатывает меню
аналогичное подменю "Формула
В.С.Ивановой в матрице". Опция "Диагонали"
предусматривает выбор значения M,
затем вводится значение R(ожидаемое
число членов ряда) . Далее
устанавливается параметр J так,
чтобы параметр m в формуле В.С.Ивановой
принимал одно из следующих значений:
1, 2, 4, 8. В левой части окна показаны
логарифмы отношений вероятностей, а
в правой отношения вероятностей в
процентах. Таблица имеет инструмент,
позволяющий изменять формат
отображаемых значений, размер ячеек
таблицы, шрифт значений. Аналогичные
возможности имеются для опции
"Стобцы", На рис.1 показан
результат работы опции "Диоганаль",
когда M = 4, R=10, J = 1 . Каждая
диагональ отмечена цветом.
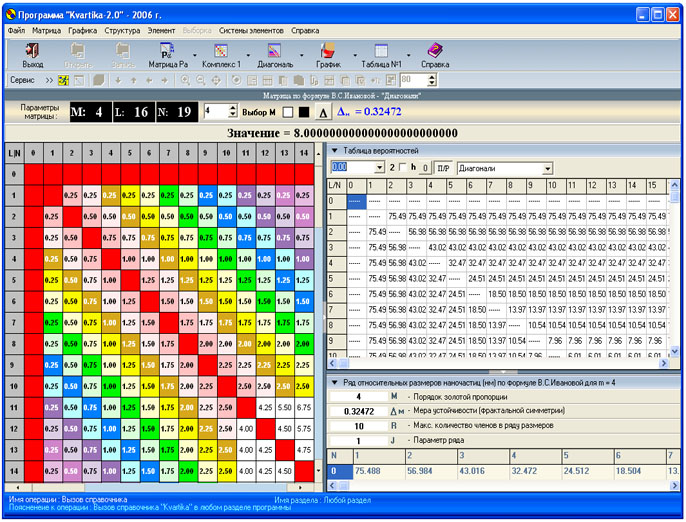
Рис.1. Результат построения
ряда размеровв опции "Диагональ"
при М=4, R=10, J=1.
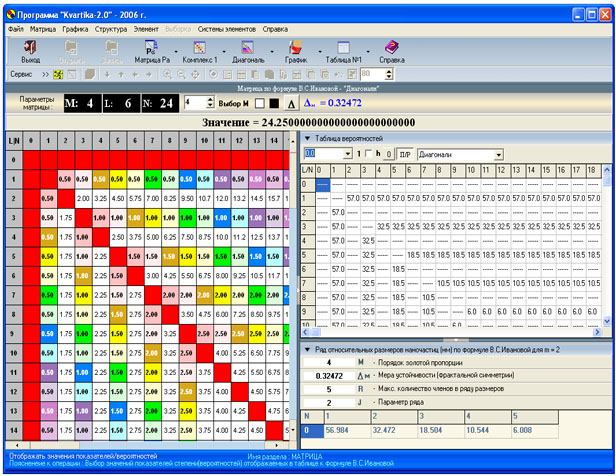
Рис.1. Результат построения
ряда размеровв опции"Диагональ"
при М=4, R=5, J=2.
Краткая теория -
Формула В.С.Ивановой в матрице
Закономерность изменения
параметров широкого класса
нелинейных наносистем в точках
неустойчивости при переходе к новой
структуре может быть представлена с
помощью формулы В.С.Ивановой [1]
 ,
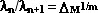где l n и
ln+1 –
предыдущее и последующее значения
параметра, например, размера системы
в процессе неравновесного фазового
перехода; 
– мера устойчивости (симметрии)
системы, взаимосвязанная с золотой
пропорцией порядка М; m –
параметр, характеризующий
особенности эволюции (обратную связь
в процессе эволюции системы), m
=1,2,4,8,16, … Порядок золотой
пропорции в матрице квантовых
измерений одновременно выполняет
две функции: во-первых, определяет
условия окружающей среды и, во-вторых,
свойства исследуемых объектов в
данных условиях [2]. Таким образом,
вероятность, соотвествующая ячейке
матрицы с координатами L , N (результату
измерения) (см. раздел «Матрица» )
определяется по формуле
 ,
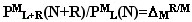где К=1 , если N
< L ; K = N - L , если N
>= L ; M,L,N = 0,1,2,… . Таким
образом, отношения вероятностей
результатов измерений,
соответствующих различным ячейкам
матрицы, можно представить в виде
аналогичном формуле В.С.Ивановой [3].
Литература
- Иванова В.С. Введение в
междисциплинарное
наноматериаловедение.- М.:«САЙНС-ПРЕСС»,
2005.-208 с.
- Чернышев С.Л., Чернышев Л.С. Логика
окружающей среды.- М.«Радиопромышленность»,
произв.-техн. сб, специальный
выпуск, 2001.
- Иванова В.С., Чернышев С.Л.
Критерии устойчивости
самоорганизующихся структур /Труды
международного симпозиума «Надежность
и качество»/ Под ред. Н.К.Юркова.-
Пенза: Изд-во ПГОУ, 2004.
|
|