Раздел "Выборка".

Раздел "Элемент" включает в себя 6 шесть подразелов:

1. "Выбор элемента" - выбор элемента из таблицы Менделеева с последующей загрузкой файла свойств элемента для таблиц №1,2;
2. "Таблица №1 Общие свойства элемента" - программа загружает по умолчанию парметры общих свойств элемента в таблицу №1 для Водорода;
3. "Таблица №2 Структура элемента" - программа загружает по умолчанию парметры свойства структуры элемента в таблицу №2 для Водорода;
4. "Построение образа элемента" - программа вызывает окно "Структура элемента" и предоставляет пользователю просмотреть все элементы периодической таблицы Менделеева, что нельзя сделать в окне "Структура элемента" в окне комплексов;
5. "Преобразования элементов" - программа в мультимедийном режиме показывает процесс образования ионов;
6. "Преобразования наноструктур".

В 1-ом подразделе вызывается таблица Менделеева, в которой выбирается элемент, далее программа по указанному элементу загружает файлы свойств элемента в таблицы №1,2 одновременно. Последнее сделано специально, чтобы можно для выбранного элемента просматривать два набора свойств элемента. На рис.1. показана окно таблицы Менделеева. В окне таблицы Менделеева имеется инструмент позволяющий проделывать математические операции с массами элементов. Для этого можно выбирать несколько элементов исходя из химической формулы и вызывать встроенный калькулятор. Для выбора элемента, который используется для загрузки свойств элемента, требуется выбрать только один элемент. Если выбрано несколько, надо оставить только один. Для этого надо нажать кнопку "Обнулить" и затем выбрать элемент. В этой версии программы данная таблица несколько устарела. В дальнейшем она будет обновлена и дополнена разрабочиком формул для проведения сложных расчетов в среде программы.

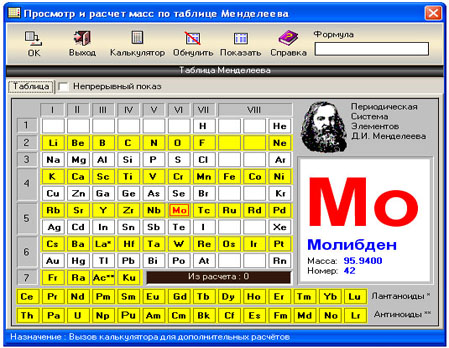
Рис.1.

После нажатия кнопки "ОК" программа перестроится и выдаст таблицу №2,3. На рис.2,3. показан вид таблицы №1,2 заполненных свойствами элемента. В целях сравнительного анализа структуры и свойств элементов таблица Д.И.Менделеева, в программе заполняются два вида таблиц свойств элементов, Система таблиц под №1 содержит справочные или полученные в результате экспериментов данные об элементах. Система таблиц №2 содержит сведения о структуре и свойствах элементов, выявленные в матрицах квантовых измерений.

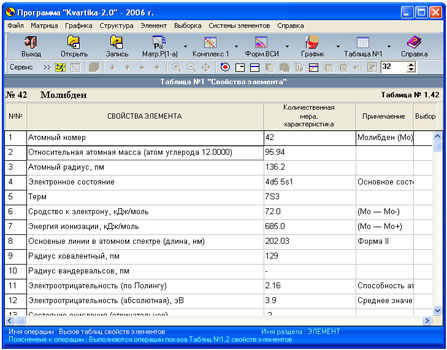
Рис.2.

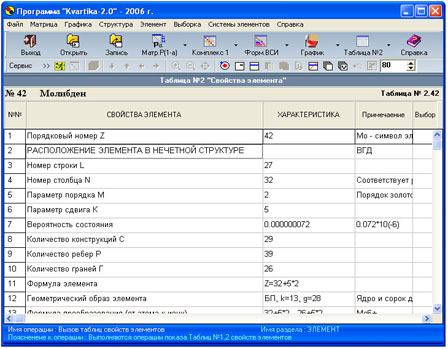
Рис.3.

Используя инструмент таблиц №1,2 пользователь может редактировать значения свойств элементов, дополнять свойства, проводить сравнительный анализ по выбранным свойствам, создавая сравнительную таблицу в программе и выдавть ее в программу MS Excel для дальнейшего анализа свойств по всем элементам.

Подразделы 2,3 ("Таблица №1 Общие свойства элемента", "Таблица №2 Структура элемента") позволяют пользователю работать со свойствами элементов. Запуская каждый из подразделов пользователь может проделывать операции кратко описанные выше.

Подразделы 5 и 6 находятся в процессе разработки.

Краткая теория

Исследования структуры и свойств нанообъектов, в том числе атомов в пространствах различных размерностей основываются на эмпирических последовательностях, взаимосвязанных с квантовыми числами [1]. Так, арифметическая прогрессия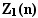 с общим элементом 2(2 n-1) определяет количество электронов, размещаемых соответственно на первой ( s -электроны), второй ( p - электроны), третьей ( d - электроны) и т.д. орбитах или подоболочках атома. Последовательность 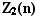с общим элементом 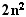показывает, сколько электронов может находиться на оболочке, характеризуемой главным квантовым числом n . Сумма вида

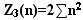
определяет суммарное количество электронов при полном насыщении всех орбит всех оболочек, с порядковыми номерами от 1 до n . Различия химических и физических свойств атомных структур с одним и тем же порядковым номером в трех- или двумерном пространствах определены в строгом соответствии с эмпирическими квантовыми последовательностями [2].Квантовые числовые последовательности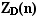,где D – максимальная степень главного квантового числа n , подчиняются следующим закономерностям. Во-первых, значение элемента 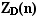при D >1 получаем, суммируя значения элементов 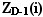, от номера 1 до номера n . Во-вторых, на основе рекуррентного соотношения 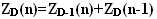могут быть получены все элементы таких последовательностей для D >1 и n >1 с учетом условий Z

.

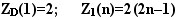Точно такими же свойствами обладают фигурные числа, с помощью которых можно представить квантовые числовые последовательности в следующем виде (см. «Комплексы в матрице» ) :

,

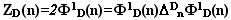где

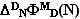
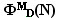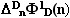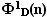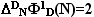— конечная разность степени D фигурных чисел вида . Здесь – значение «единицы измерения» (вида «орта») в D -мерном пространстве; – числовое значение величины. При этом . Из этого выражения следует, что степень квантовой числовой последовательности D равна размерности пространства.

В разделе «Элемент» представлены следующие подразделы:

• Элементы в комплексах . В этом подразделе элементы, характеризуемые порядковыми номерами, размещаются в комплексах матрицы. В соответствии с положениями элементов определяется их структура и производится классификация элементов (см. «Системы элементов» ).
• Свойства элементов . В более, чем 200 таблиц собраны оригинальные (на основе положения в матрицах), а также справочные сведения об элементах. Предусмотрена возможность пополнения таблиц (до 200 характеристик исследуемых объектов в каждой), а также передачи сводных данных таблиц в формате Excel для последующей обработки.
• Преобразования элементов . Предполагается демонстрация операций понижения или повышения размерности фигурного числа, представляющего модель атома, при сохранении порядка золотой пропорции М , определяющего симметрию модели.
• Преобразования наноструктур . Предполагается демонстрация возможностей синтеза многоядерных структур с использованием аппарата произведения стохастических матриц (см. «Операции» ) .

Литература

• Блохинцев Д.И. Основы квантовой механики.-СПб.: Изд-во «Лань», 2004.
• Negadi T., Kibler M. The Periodic Table in Flatland // Intern. Journal of Quantum Chemistry, Vol. 57, 1996, №1. p.53-61.
• Чернышев С.Л., Чернышев Л.С. Квантовый анализ результатов измерений// Измерительная техника, 2006, №12.
• Чернышев С.Л. Квантовый анализ атомных структур на основе четырехзначной логики измерений// Нелинейный мир, 2006, №11.