| |
подраздел "Образы
элементов".
В меню "Элемент"
опцией "Построение образов
элементов" и на странице "Быстрый
Вход" вызывается окно "Структура
элемента". Это окно
аналогично окну, которое вызывается
при просмотре комлекса. Отличие
заключается лишь в больших
возможностях. В комплексах окно "Структура
элемента" можно посмотреть
образ только для одного элемента, а
здесь можно просмотреть образы для
всех элементов в 2-х мерном и 3-х
мерном пространстве. На рис.1.
показано окно "Структура
элемента" , которое вызвано из
страницы "Быстрый Вход" или
опцией "Построение образов
элементов" из меню "Элемент".
В верхней части окна над
изображением образа (стрктуры)
элемента располагаются кнопки
слевой и правой стрелками. С их
помощью пользователь может
просмотреть все образы элементов и
парметры описывающих их. Под
изображением образа элемента
кнопкой "2D/3D" можно
назначать просмотр образов
элементов в 2-х и 3-х мерном
пространстве. Под изображением
образа элемента располагается
таблица парметров описывающая
структуру образа элемента. Таблица
разбивается на две страницы "Параметры
положения" и "Параметры
структуры" . Над таблицей
отображается в каком пространстве
находится элемент в двухмерном или
трех мерном. На странице "Параметры
положения" отображается
координата элемента в матрице, т.е.
даются значения номеров столбцов N
и номеров строк L. И плюс к
этому отображается порядок золотой
пропорции M. На странице "Параметры
структуры" отображаются
параметры :
- k - число углов в
основании пирамиды и
соответствует симетрии фигурного
числа - образу элемента;
- С - число
конструкций графа;
- Р- число ребер
графа;
- Г - количество
односвязных областей.
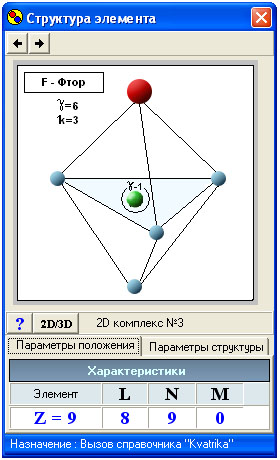
Рис.1.
Краткая теория
Каждому элементу матрицы,
расположенному в L -й строке
и N -м столбце, при заданном
значении порядка золотой пропорции М
соответствует фигурное число
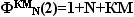 , ,
где К=1 , если N
< L ; К= N - L , если N
>= L . На главной диагонали
матрицы (здесь К=0 при любом
значении параметра М)
фигурные числ а 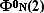 представляют собой симплексы в
евклидовых пространствах с
размерностью N , то есть точку
представляют собой симплексы в
евклидовых пространствах с
размерностью N , то есть точку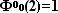 ,
отрезок ,
отрезок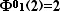 , треугольник
, треугольник 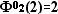 ,
тетраэдр ,
тетраэдр 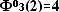 и т.д. Треугольные фигурные числа
показаны на рисунке.
и т.д. Треугольные фигурные числа
показаны на рисунке.
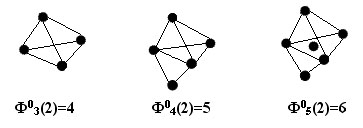
Для фигурных чисел вида 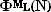 значение М = 0 соответствует
треугольным числам, значение М=1
- четырехугольным; М=2 -
пятиугольным и т.д. Таким образом,
количество k углов
многоугольника, образующего
фигурное число, и значение параметра
M взаимосвязаны соотношением
k =М+3 .
значение М = 0 соответствует
треугольным числам, значение М=1
- четырехугольным; М=2 -
пятиугольным и т.д. Таким образом,
количество k углов
многоугольника, образующего
фигурное число, и значение параметра
M взаимосвязаны соотношением
k =М+3 .
Для N = 4 новая точка при
отображении в трехмерном
пространстве образует симметричную
относительно основания пирамиды
вершину. Для N >4 новая
точка слипается с одной из точек
фигуры. При этом не нарушается
фрактальная симметрия,
характеризуемая прядком золотой
пропорции М .
Фигурные числа — результаты
квантовых измерений — представляют
собой собственные функции
операторов конечных разностей
по N и L . Собственные
значения для этих операторов равны
единице ( при N не
равном L ).
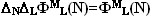 или или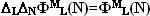
Фигурное число Ф М L ( N ) (целый
неотрицательный образ трехмерного
неотрицательного целочисленного
вектора { L , N ,М} ) может быть
задано рекуррентным соотношением
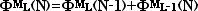 . .
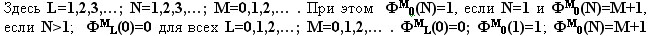 при
N >1 . Переменные М и
L указаны в виде индексов. при
N >1 . Переменные М и
L указаны в виде индексов.
Литература
- Математическ ий энциклопеди
ческий словарь . - М.: Научное
издательство «Большая Российская
энциклопедия», 1995.
- Чернышев С.Л., Чернышев Л.С. Логика
окружающей среды.- М.«Радиопромышленность»,
произв.-техн. сб, специальный
выпуск, 2001.
- Чернышев С.Л. Представление
квантовых числовых
последовательностей с помощью
комбинаторных чисел/ Надежность и
качество. Труды международного
симпозиума. В 2-х томах /Под ред. Н.К.Юркова.-
Пенза: Изд-во Пенз.гос.ун-та,. 2006, Т.1.,
с.314.
|
|