Раздел "Матрица".

В разделе "Матрица" выполняется построение матриц и просмотр каждой ячейки (элемента) матрицы. На рис.1. показан общий вид состояния программы в разделе "Матрица". Для просмотра матриц с различными параметрами пользователь может использовать меню опции "Матрица" или кнопку-меню "Матрица..." верхней инструментальной доски. Используя пять опций меню или кнопки-меню, нажатием которых пользователь может получить пять различных числовых представлений матрицы:

• для вероятностей Рa;
• для веротяностей Р(1- a);
• для логарифмов вероятностей по основанию aм;
• для логарифмов вероятностей по основанию 1- aм - (Фигурные числа);
• для логарифмов вероятностей по основанию Dм
•  

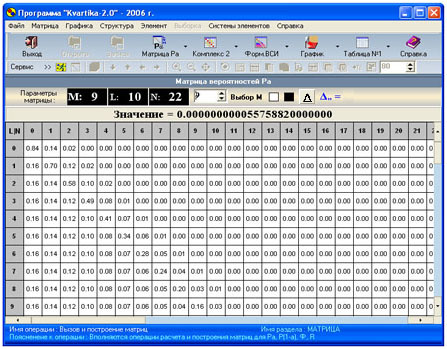
Рис.1.

Программа производит расчет элементов матрицы для установленного параметра М. По умолчанию параметр М всегда равен 0. Параметр М устанавливается на инструментальной доске раздела, которая располагается над окном матрицы. Для получения значения элемента матрицы с максимальной точностью пользователю надо подвести курсор на этот элемент(клетку). Тогда над окном матрицы появится индикация этого значения Для просмотра элементов матрицы применяются средства прокрутки, располагающиеся справа и нижней части окна матрицы. Для выделения элемента различными цветами используются кнопки раскраски клеток матрицы и раскраски текста в клетках, располагающиеся рядом с окошком установки параметра М. Щелчок курсора на эти кнопки вызывает диалоговое окно "Цвет". Индикация цвета представлена на самих кнопках. По умолчанию они имею "Черный" и "Белый" цвет. На рис.2. показан участок матрицы с раскрашенными элементами. При перемещении курсора по плоскости матрицы программа отображает значения каждого элемента матрицы с большой точностью (24-е знака после запятой) и координаты значения, т.е. номера столбцов N и строк L.. Рядом кнопками раскраски элементов находится кнопка DM. Щелчок данной кнопки дает еще одну форму числовому представления матрицы связанную с формулой В.С.Ивановой.(см. "Краткая теория") - Это пятый способ представления матрицы.

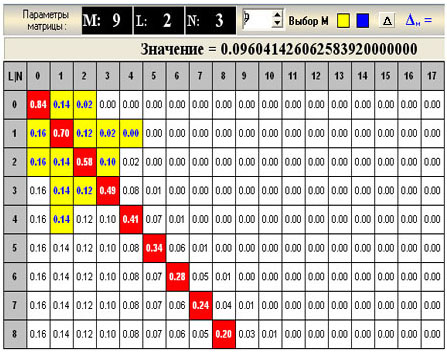
Рис.2.

Краткая теория

 Воздействие окружающей среды и измерение — процессы, связанные с необратимостью времени и необходимостью одновременно рассматривать не отдельные объекты или траектории, а их множества, то есть коллективные явления . Представление воздействий и измерений существенным образом опирается на понятие вероятности, представляющей элемент «новой обобщенной рациональности» [1]. Характерное проявление воздействий окружающей среды — отклонение от равновесного состояния, возникновение неустойчивости, приводящее к появлению фрактальных структур [1-3].Дискретная динамическая модель измерений - воздействий [4,5] основана на последовательном сравнение неотрицательного целого значения L с “мерами“- целым и неотрицательным и числами N =0,1,2,…, начиная с нуля. Вероятности ошибок, не зависящие от номера N этапа сравнения, характеризуют условия проведения измерений (окружающей среды). Результаты измерений представляет стохастическая матрица-оператор бесконечного порядка

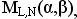
преобразующая исходное распределение вероятностей измеряемой величины в распределение измеренного значения. В этом процессе на этапах сравнения реализуются четыре вида решений (логических состояний), показанных в таблице. (см. рис.3.)

Рис.3

Для рассматриваемой матрицы характерны отличные от нуля элементы вне главной диагонали. Именно такие элементы, обусловленные воздействием окружающей среды, ответственны за возникновение новых структур, исследуемых в мультимедийном комплексе. При значениях параметров a,b, взаимосвязанных с золотыми пропорциями, каждому элементу матрицы (называемой в данном случае матрицей квантовых измерений ) соответствует результат измерения — комбинаторный объект в виде фигурного числа. Построение матриц. Показаны 75 стохастических матриц (75 строк и 75 столбцов в каждой). Приведены пять вариантов числового выражения элементов матриц. Графика . Матрицы (выбранные строки и столбцы) графически отображаются дву- или трехмерным способом. Образы элементов. Предполагается демонстрация образа любого элемента (ячейки) матрицы, т.е. результата квантового измерения в виде фигурного числа. Операции. Предполагается демонстрация произведений дискретных распределений вероятностей (записанных в виде строки) на матрицу, а также матрицы на матрицу.

Литература

1. Пригожин И. Конец определенности. Время, хаос и новые законы природы/ Пер.с англ- Ижевск: НИЦ «Регулярная и хаотическая динамика».-2001.
2. Иванова В.С. и др. Синергетика и фракталы в материаловедении. М.: Наука, 1994.
3. Николис Г., Пригожин И. Познание сложности/ Пер. с англ.- М.:Мир, 1990.
4. Чернышев С.Л., Дмитриев А.С. Модель неспецифического воздействия окружающей среды. Препринт ИРЭ РАН, 4(604), 1995.
5. Чернышев С.Л., Чернышев Л.С. Квантовый анализ результатов измерений/ Измерительная техника, 2006, №12.

Построение матриц

В разделе "Матрица" программа воспроизводит стохастические матрицы квантовых измерений. На экране дисплея представлены 75 строк (с номерами от 0 до 74) и 75 (с номерами от 0 до 74) столбцов матрицы. Номера строки L и столбца N указываются в окнах для положения курсора, находящегося в определенной ячейке матрицы. Одновременно вычисляется содержимое ячейки: строка с указанием «Значение».

Для работы в разделе «Матрица» прежде всего необходимо выбрать значение параметра порядка М (порядок золотой пропорции) в соответствующем окне. При этом устанавливаются равные значения вероятностей ошибок (aм = bM) ,взаимосвязанные с отношением золотой пропорции q м порядка М формулами:

qМ = 1/(1- aм);

qМ = 1/(1- bM).

После этого с помощью соответствующих «иконок» можно выбрать вид (числовую форму) представления ячеек матрицы. Имеется пять возможностей.

1. При выборе «иконки» Рa вычисляются вероятности Р М, L ( N ), соответствующие ячейке матрицы ML,M (aм,bM) и выбранному значению параметра порядка М, определяемые по формуле

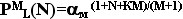
где К = 1, если N < L ; K = N - L , если N >= L ; M,L,N=0 ,1,2,… .

2. При выборе «иконки» Р 1- a вычисляются вероятности Р М L ( N ), соответствующие ячейке матрицы ( L , N ) и выбранному значению параметра порядка М, определяемые по формуле

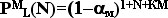
Оба указанных способа представления вероятностей идентичны. Малые расхождения обусловлены точностью вычисления параметра aм . Суммы по N вероятностей 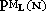в каждой строке L каждой матрицы M равны единице, т.е. выполнено условие стохастичности матриц.

3. При выборе «иконки» Ф вычисляются логарифмы вероятностей 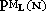по основанию 1- a м представляющие собой фигурные числа вида

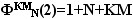
4. При выборе «иконки» R вычисляются логарифмы вероятностей 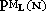по основанию aм представляющие собой рациональные числа (1+ N + K M)/(М+1).

5. При нажатии кнопки DM вычисляются логарифмы вероятностей Р М L ( N ) по основанию DM , где DM = aм / (1- aм ) или DM = bM / (1- bM), то есть рациональные числа вида (1+ N + KM)/М . Этот способ представления элементов матрицы применяется для демонстрации формулы В.С.Ивановой, отражающей закономерность преобразования наноструктур, например, для прогнозирования последовательностей устойчивых размеров наночастиц (см. "Формула В.С.Ивановой в матрице").

Литература

1. Иванова В.С. Введение в междисциплинарное наноматериаловедение. М.: «САЙНС-ПРЕСС», 2005,-208 с.
2. Чернышев С.Л., Чернышев Л.С. Логика окружающей среды.- М.«Радиопромышленность», произв.-техн. сб, специальный выпуск, 2001.
3. Чернышев С.Л. Измерение как обобщенное воздействие // Измерительная техника. 2003, №8, с.11.
4. Чернышев С.Л., Чернышев Л.С. Квантовый анализ результатов измерений//Измерительная техника, 2006, №12.