Подпрограмма "Элементы в комлексах".

При нажатии кнопки "Установить/Отменить показ образа элемента программа вызывает окно отображения образа элемента. Окно отображения комплекса имеет две прокрутки, позволяющие пользователю просмотреть весь комплекс. На рис. 1 показано окно с образом элемента, где кроме графического образа отображается таблица парметров описывающая структуру образа элемента. Таблица разбивается на две страницы "Параметры положения" и "Параметры структуры" . Над таблицей отуказана мерность D модельного пространства. На странице "Параметры положения" отображается координата элемента в матрице, т.е. даются значения номеров столбцов N и номеров строк L. И плюс к этому отображается порядок золотой пропорции M. На странице "Параметры структуры" отображаются параметры :

• k - число углов в основании пирамиды и соответствует симетрии фигурного числа - образу элемента;
• g - число слипшихся точек, которые могут находится в одной и той же вершине (g = С ) ;
• С - число конструкций графа;
• Р- число ребер графа;
• Г - количество односвязных областей.

Образ элемента в комлексе вызывается щелчком на элемент в комплексе. Настоящая подпрограмма показывает не только образ элемента, на который указал курсор, но и образы соседних элементов. Просмотр образов соседних элементов обеспечивается кнопками с горизонтальными стрелками. Кнопки располагаются над окном образа элемента.

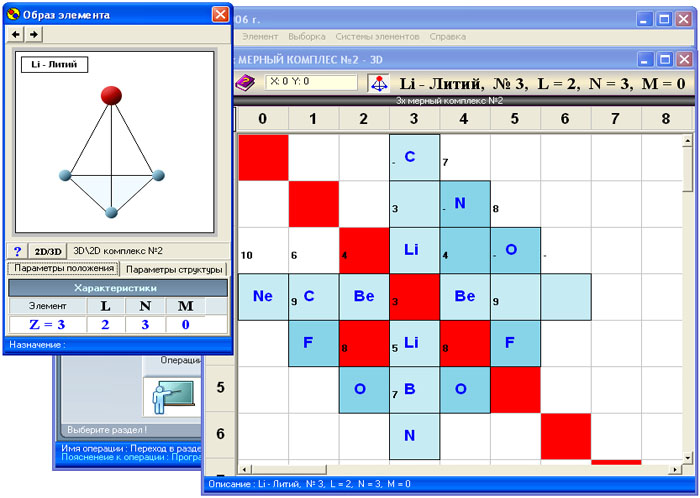
Рис.1.

Краткая теория

При размещении элементов, характеризуемых порядковым номером , в определенных структурах и комплексах матрицы выявляются новые свойства этих элементов, дополняющие известные результаты [1]. Образом элемента с порядковым номером Z в матрице может служить симплекс, то есть фигурное число

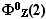
(см. "Образы элементов"), включающий Z +1 точку, одна из которых — ядро. Порядковый номер элемента в этом случае равен «расстоянию от ядра»:

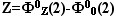[2].

Отображение элемента (порядкового номера Z ) в комплексы матрицы приводит к соотношению

,

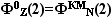которое означает равенство вероятностей

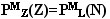
в матрице квантовых измерений и показывает, что порядок золотой пропорции М является инвариантом отображения. При этом Z = N +КМ , где К=1 , если N < L ; К= N - L , если N >= L . Здесь L – номер строки матрицы (измеряемая размерность); N – номер столбца матрицы (измеренная размерность); М – порядок золотой пропорции, определяющий условия измерений. Параметры L , M и N – неотрицательные целые числа. Таким образом, каждому элементу Z , помещенному в определенную ячейку матрицы, соответствует определенное фигурное число, которое может быть представлено с помощью графа. Приняты следующие обозначения: C – количество конструкций графа; P – количество ребер графа; Г – односвязных плоских областей (граней) графа. При этом Z = В - 1 , где В - число вершин графа, отображающего данное состояние элемента. При этом не связанные точки, составляющие фигурное число, представляют самостоятельные конструкции графа. Такие точки появляются в следующих случаях: 1) если N =0 (т.е. геометрический образ фигурного числа находится в пространстве нулевой размерности); 2) если N >4 , то каждая новая точка, которая добавляется к фигурному числу, представляет собой не связанную точку. Полагаем, что при отображении в трехмерном пространстве эта новая точка (значение N увеличивается на единицу) может слипаться с одной из точек фигурного числа меньшей размерности [3]. Параметры С, Р, Г связаны с порядковым номером элемента следующим соотношением Z =С+Р-Г . При С=1 с учетом равенства Z = В -1 приходим к известному соотношению Эйлера для выпуклых многогранников В-Р+Г=2. Количество углов многоугольника, лежащего в основании фигурного числа определено соотношением k =КМ+3 . Максимальное число слипшихся в одну точек обозначим g . Тогда при наличии слипшихся точек выполняется условие Z = k + g .

Литература

1. Блохинцев Д.И. Основы квантовой механики.-СПб.: Изд-во «Лань», 2004.
2. Чернышев С.Л. Измерение как обобщенное воздействие//Измерительная техника, 2003, №8, с.11.
3. Чернышев С.Л. Квантовый анализ атомных структур на основе четырехзначной логики измерений// Нелинейный мир, 2006, №11.
4. Акимов О.Е. Конструктивная математика. — М.:Издатель АКИМОВА, 2005.