подраздел "Периодическая система элементов в двумерном пространстве".

  Периодическая система элементов в двумерном пространстве впервые определена в [1]. В основе ее построения — квантовые числовые последовательности, а также обобщенное правило Маделунга для D -размерности и принцип исключения Паули [2]. При этом количество групп элементов не ограничено.

Построение квантовой степенной шкалы на основе теории вычетов приводит к таблице, содержащей 10 групп (классов эквивалентности) элементов в зависимости от их удаления от фиксированных номеров-реперов. Реперы квадратичной шкалы определяются квантовой числовой последовательностью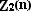, а также путем отображения подобных элементов в комплексах матрицы на главную диагональ матрицы [3,4]. Предполагается демонстрация этого построения, приводящего к линеаризации квадратичной шкалы, мультимедийными средствами в программе.

Все реперы квадратичной шкалы разделяются на два класса: с характеристиками 4 и 6 в виде разностей ближайших по порядку реперов. В результате подсчета всевозможных удалений от реперов двух указанных классов получаем 10 групп (классов эквивалентности) элементов. Такие классы эквивалентности различаются индексами вида ( i , j ), где число i означает удаление (разность), а число j характеристику репера. Распределение элементов по группам и периодам, показанное в настоящем разделе программы соответствует варианту Периодической системы [1] для первых тридцати элементов ( за исключением положения первого и второго элементов). Отметим, что классификация элементов в степенной шкале не зависит от порядка золотой пропорции М , характеризующего условия окружающей среды.

Основное расхождение с результатами [1], проявляется после 30 номера элемента. Это расхождение обусловлено тем, что построение квадратичной шкалы на главной диагонали матрицы приводит к конечному числу групп элементов. Это означает, что в Периодической системе в виде квадратичной шкалы есть только s -, p - и d - элементы, а элементы, соответствующие значениям орбитального квантового числа 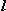> 2, в частности, f - элементы отсутствуют [3,4] .

Заметим, что особые свойства проявляли бы элементы с порядковыми номерами, равными реперам квадратичной шкалы. Индексы групп для этих элементов имеют вид (0,6), (0,4) и соответствуют порядковым номерам 2, 8, 14, 18, 24, 28, 32, 38, 42, 46, 50, 56, 60, 64, 68, 72, 78, 82, 86, 90, 94 и т.д. Так, например, аналогично свойству инертности атомов неона и аргона в кубической шкале, «свойство инертности» проявляли бы кислород и кремний в квадратичной шкале. В то же время в плоском мире элементы с порядковыми номерами 36 (криптон) и 54 (ксенон) теряют данное свойство.

Литература

1. Negadi T., Kibler M. The Periodic Table in Flatland // Intern. Journal of Quantum Chemistry, Vol. 57, 1996, №1. p.53-61.
2. Кораблева Т.Г., Корольков Д.В. Развитие теории Периодической системы во второй половине ХХ в. // Вестник МГУ.Химия.-2002.Т.43
3. Чернышев С.Л., Чернышев Л.С. Квантовый анализ результатов измерений//Измерительная техника, 2006, №12.
4. Чернышев С.Л. Моделирование структуры и свойства элементов в дву- и трехмерных евклидовых пространствах.— М.:Радиопромышленность, произв.-техн. сб., 2006, вып.2, с.156.