
|
Недоопределённые множества это новая разновидность структур данных (термов), изобретённая в Акторном Прологе. Они немного напоминают так называемые структуры и записи, используемые в императивных и некоторых логических языках, однако выразительные возможности недоопределённых множеств значительно выше. Дело в том, что недоопределённые множества, в отличие от записей, могут помимо явно указанных элементов включать неопределённый остаток (хвост), так как это происходит со списками в обычном Прологе. При этом, однако, порядок элементов в недоопределённом множестве может быть произвольным и не влияет на результаты унификации этих термов. Более того, в Акторном Прологе гарантируется, что остаток недоопределённого множества не может содержать элементы, явно заданные в составе множества. То есть язык обеспечивает проверку некоторых негативных условий, наложенных на остаток недоопределённого множества. Недоопределённые множества являются очень мощным средством логического программирования. Они были разработаны специально для решения задач, требующих имитации логики второго порядка. При этом их реализация достаточно проста и эффективна, потому что не требует использования унификации высших порядков или механизма ограничений. Рассмотрим пример Sets.A. Пример 1. Недоопределённые множества.
-------------------------------------------
-- An example of Actor Prolog program. --
-- (c) 2002, Alexei A. Morozov, IRE RAS. --
-- Underdetermined sets. --
-------------------------------------------
project: (('Sets'))
-------------------------------------------
class 'Sets':
con = ('Console');
[
goal:-
A == { region:X,
name:"Baikal"
|Rest},
--
B == { name:Y,
object:'lake',
region:"Siberia"},
--
A == B,
--
con ? writeln("Region: ",X),
con ? writeln("Name: ",Y),
con ? writeln("Rest: ",Rest).
]
-------------------------------------------
В рассматриваемом примере осуществляется унификация двух недоопределённых множеств. Элементами недоопределённых множеств в Акторном Прологе являются пары, состоящие из имени и значения. Так, первое недоопределённое множество (A) содержит два элемента region и name, а также неопределённый остаток Rest. Значением первого элемента является переменная X, а значением второго строковый литерал "Baikal". Второе недоопределённое множество (B) содержит три элемента name, object и region. Значением первого элемента является переменная Y, значением второго символ 'lake', а значением третьего строковый литерал "Siberia". Результаты работы программы:
Region: Siberia
Name: Baikal
Rest: {object:'lake'}
В ходе унификации множеств осуществляется сопоставление значений элементов с одинаковыми именами. В нашем примере переменная X будет унифицирована со строкой "Siberia", а переменная Y со строкой "Baikal". Кроме того, остаток первого множества Rest будет сопоставлен с оставшимися элементами второго множества. В результате значением переменной Rest станет недоопределённое множество, содержащее один элемент 'lake'. Обратите внимание, что созданное множество Rest не имеет неопределённного остатка, потому что его не было у множества B. Это означает, в частности, что переменная Rest уже не может быть унифицирована с другими множествами, содержащими какие-либо элементы, отличные от object. В Акторном Прологе можно использовать "неопределённые множества с заголовком" вида
Heading{...}
При этом терм Heading будет обозначать добавочный элемент 0:Heading с именем 0. Можно использовать недоопределённые множества в качестве атомарных формул в предложениях языка. Например, атомарная формула
F { sX:AX, sY:AY, ..., sN:AN | Rest }
будет эквивалентна атомарной формуле
''( { 0:F, sX:AX, sY:AY, ..., sN:AN | Rest } )
где '' - специальный символ, состоящий из пустой цепочки графем.
С помощью таких атомарных формул можно составлять логические правила, имитирующие логику второго порядка. Рассмотрим, например, (упрощённое) правило использования конструкции ветвления, написанное для программы синтеза алгоритмов. Пример 2. Имитация логики второго порядка.
F{argument:A0,result:Z|Rest}:-
A0 == {even:'unknown'|Pairs},
A1 == {even:'yes'|Pairs},
A2 == {even:'no'|Pairs},
F{argument:A1,result:Y1|Rest},
F{argument:A2,result:Y2|Rest},
Z == 'if'([
guard(odd(A0),Y2),
guard(even(A0),Y1)]).
Это правило используется, если программа не знает, как реализовать вычисление функции F с некоторым аргументом argument, про который известно, что он может быть как чётным, так и нечётным. В этом случае возможным решением является построение конструкции if-fi. Для этого создаются две новые переменные A1 и A2. Эти переменные получают все свойства аргумента A0 за исключением признака чётности. Переменная A1 объявляется чётной, а переменная A2 нечётной. Если программа сможет найти метод вычисления функции F отдельно для любых чётных и любых нечётных значений аргумента argument, будет синтезирован оператор if-fi, вычисляющий значение исходной функции F. Пример 3. Программа синтеза алгоритмов.В качестве иллюстрации использования недоопределённых множеств, далее приведён полный текст программы, синтезирующей алгоритмы умножения. Постановка задачи. Необходимо синтезировать алгоритмы умножения двух целых положительных чисел на основе операций сложения и сдвига. Полученные алгоритмы записать на языке Ада. Текст программы на Акторном Прологе, синтезирующей алгоритмы умножения, приведён здесь. Обратите внимание, как реализованы правила синтеза ветвлений и инвариантов циклов. |
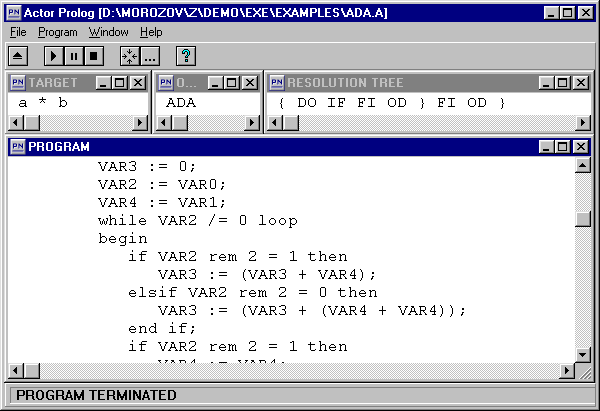
Рис. 3.1. Синтез алгоритмов умножения.
|
Результаты синтеза приведены здесь. Самое интересное, что программа доказала существование двух алгоритмов умножения, отвечающих заданным условиям. Второй из них вполне обычный, а вот первый оказался неожиданным. |

|
Оглавление |

|