
|
Underdetermined sets is a new type of data structures (terms) developed in Actor Prolog. They resemble so-called structures and records commonly used in imperative and some logic languages. However the expressiveness of the underdetermined sets is noticeably higher. The point is that an underdetermined set can include some indefinite rest (a tail) like a list in usual Prolog. At the same time, the order of elements of an underdetermined set can be arbitrary one and it does not affect results of unification of underdetermined sets. Moreover, Actor Prolog guarantees that a rest of an underdetermined set never contains elements that are explicitly given in the set. In other words, the language provides for a check of some negative conditions imposed on the rest of an underdetermined set. The underdetermined sets are very powerful means of logic programming. They were elaborated specially for solving problems demanding an implementation of second order logic. At the same time implementation of underdetermined sets is quite simple and effective, because it requires no higher order unification or constraints. Let us consider the Sets.A example. Example 1. Underdetermined sets.
-------------------------------------------
-- An example of Actor Prolog program. --
-- (c) 2002, Alexei A. Morozov, IRE RAS. --
-- Underdetermined sets. --
-------------------------------------------
project: (('Sets'))
-------------------------------------------
class 'Sets':
con = ('Console');
[
goal:-
A == { region:X,
name:"Baikal"
|Rest},
--
B == { name:Y,
object:'lake',
region:"Siberia"},
--
A == B,
--
con ? writeln("Region: ",X),
con ? writeln("Name: ",Y),
con ? writeln("Rest: ",Rest).
]
-------------------------------------------
In the example a unification of two underdetermined sets is fulfilled. In Actor Prolog elements of underdetermined sets are pairs composed of a name and a value. Thus, the first underdetermined set A contains two elements region, name, and also an indefinite tail Rest. The value of the first element is the variable X, the value of the second one is the "Baikal" string. The second underdetermined set B contains three elements: name, object, and region. The value of the first element is the variable Y, the value of the second one is the 'lake' symbol, and the value of the third one is the "Siberia" string. The results of the program are the following:
Region: Siberia
Name: Baikal
Rest: {object:'lake'}
In the course of the unification of the underdetermined sets computer compares the elements with equal names. In the example under consideration the variable X is unified with the "Siberia" string and the variable Y is unified with the "Baikal" string. Moreover, the Rest tail of the first set is compared with the remaining elements of the second one. As a result the value of the variable Rest becomes a new underdetermined set containing one 'lake' element. Note that the created set Rest does not contain a tail because the set B does not contain any indefinite tail. So, the variable Rest could not be unified with a set containing some additional elements. One can use the underdetermined sets with a "heading" in Actor Prolog:
Heading{...}
In this case the Heading term denotes some additional element 0:Heading with the 0 name, in the structure of the set. One can use an underdetermined set as an atomic formula in clauses of a program. For instance, the atomic formula
F { sX:AX, sY:AY, ..., sN:AN | Rest }
is identical to the atomic formula
''( { 0:F, sX:AX, sY:AY, ..., sN:AN | Rest } )
where '' is a special symbol containing empty series of character symbols.
One can write clauses imitating second order logic rules with the help of these atomic formulas. Let us consider some (simplified) rule of application of the if-fi branching operator written for a program that synthesizes algorithms. Example 2. Imitation of second order logic.
F{argument:A0,result:Z|Rest}:-
A0 == {even:'unknown'|Pairs},
A1 == {even:'yes'|Pairs},
A2 == {even:'no'|Pairs},
F{argument:A1,result:Y1|Rest},
F{argument:A2,result:Y2|Rest},
Z == 'if'([
guard(odd(A0),Y2),
guard(even(A0),Y1)]).
The program uses this rule for implementing a computation of a function F with some argument that can be even or odd. A possible result of computation could be creation of some if-fi operator. For this purpose two new variables A1 and A2 are created. These items get all properties (all the content) of the argument A0 with the exception of the even element. In addition, the variable A1 is declared as even one and the variable A2 is declared as odd one. Now if the program find methods of computation of the function F separately for any even values of the argument and for any odd values of the argument, the if-fi operator is created. This operator will compute the function F in all the cases. Example 3. Synthesis of algorithms.Let us consider the complete text of the program that synthesizes algorithms. Target setting. The program must synthesize algorithms of multiplication of two positive integer numbers, using only the shift and adding operations. The algorithms must be written in the Ada language. One can see the text of the program written in Actor Prolog here. Note that the rules of creation of branches and cycles are implemented with the help of some second order rules. |
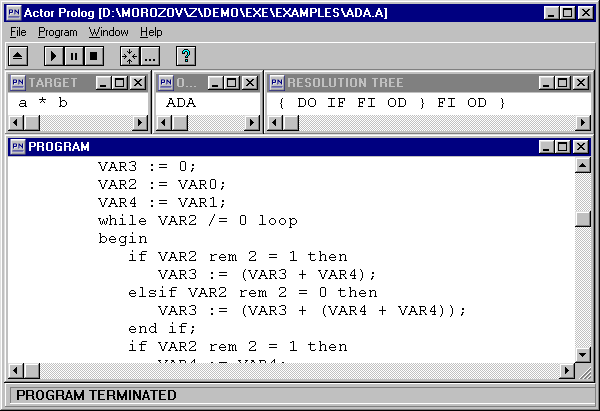
Fig. 3. Synthesis of multiplication algorithms.
|
One can see the results of the program here. The point is that the program has proven existence of two multiplying algorithms. The second one is quite ordinary, but the first algorithm turned out unexpected one. |

|
Table of content |

|