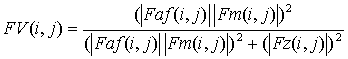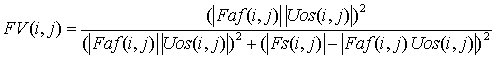УДК 621.396
Использование универсального опорного спектра для оценки отношения шум – сигнал в фильтре Винера
А. В. Кокошкин, В. А. Коротков, К. В. Коротков, Е. П. Новичихин
Институт радиотехники и электроники им. В.А. Котельникова РАН,
Фрязинский филиал
Статья получена 22 июня 2015 г.
Аннотация. В этой работе предлагается модификация фильтра Винера на основе универсального опорного спектра. Это позволяет восстанавливать искажённые изображения с неизвестными аддитивными шумами и помехами.
Ключевые слова: универсальный опорный спектр, фильтр Винера, шумы, помехи.
Abstract. A modification of the Wiener filter using a universal reference spectrum is proposed in the paper. This allows to restore the distorted image with unknown additive noise and interference.
Key words: universal reference spectrum, the Wiener filter, noise, interference.
Введение
Решение задачи восстановления искаженных изображений при наличии шума предполагает использование тех или иных методов регуляризации (регуляризация по Тихонову, фильтр Винера, метод перенормировки с ограничением) [1 – 6, 9]. Для применения фильтра Винера (ФВ) [1 – 3] необходимо знать отношение спектральных мощностей шума к сигналу в отсутствие шума. Обычно имеются самые общие представления о спектральных характеристиках шума и сигнала. Часто просто предполагают, что отношение не зависит от частоты, то есть является константой K, которую подбирают, исходя из целей восстановления изображения.
В данной работе демонстрируется возможность использовать универсальный опорный спектр (УОС) [8, 13] в фильтре Винера для оценки как спектра изображения, так и спектра шума.
Фильтр Винера справедлив для аддитивного статистически независимого от изображения шума, среднее значение которого равно нулю. Рассмотрим некоторые частные варианты таких помех и шумов.
1. Флуктуационный некоррелированный шум
Некоррелированный шум характеризуется дисперсией, для определения которой можно построить простой алгоритм, основанный на измерении корреляционной функции наблюдаемого изображения [4 – 6]. В этих работах показано, что корреляционная функция наблюдаемого изображения отличается от корреляционной функции незашумленного изображения только в начале координат, и это отличие равно дисперсии шума:
![]() , (1)
, (1)
где ![]() —дисперсия
шума,
—дисперсия
шума, ![]() и
и ![]() -
корреляционные функции зашумленного и незашумленного изображения
соответственно. Вблизи начала координат (k=0, l=0)
эти корреляционные функции являются весьма медленно меняющимися функциями k и l [4 – 6]. Поэтому величину
-
корреляционные функции зашумленного и незашумленного изображения
соответственно. Вблизи начала координат (k=0, l=0)
эти корреляционные функции являются весьма медленно меняющимися функциями k и l [4 – 6]. Поэтому величину ![]() , необходимую для вычисления дисперсии некоррелированного
шума по (1), можно с высокой точностью оценить экстраполяцией по значениям
, необходимую для вычисления дисперсии некоррелированного
шума по (1), можно с высокой точностью оценить экстраполяцией по значениям ![]() в точках k и l,
вблизи нуля. Таким образом, для определения дисперсии аддитивного
некоррелированного шума на изображении достаточно измерить корреляционную
функцию
в точках k и l,
вблизи нуля. Таким образом, для определения дисперсии аддитивного
некоррелированного шума на изображении достаточно измерить корреляционную
функцию ![]() наблюдаемых изображений в малой
окрестности вблизи точки 0, найти экстраполяцией оценку
наблюдаемых изображений в малой
окрестности вблизи точки 0, найти экстраполяцией оценку ![]() величины
величины ![]() и
принять в качестве оценки дисперсии величину
и
принять в качестве оценки дисперсии величину
![]() . (2)
. (2)
Эксперименты показывают [4], что хорошая оценка получается даже при экстраполяции по одномерным сечениям корреляционной функции [4-6].
Рассмотрим, как работает этот метод, на примере изображения на рис.1.

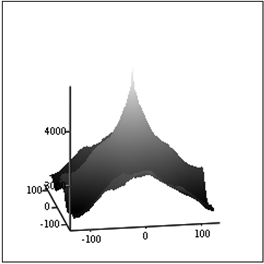
А Б
Рис.1. Исходное изображение – А и его автокорреляционная функция – Б.
Добавим к изображению на рис.1А Гауссов нормальный шум со средним значением, равным нулю, и среднеквадратичным отклонением Si=10. На рис.2 представлен график разрезов автокорреляционных функций изображения рис.1А и изображения рис.1А с добавленным нормальным шумом.
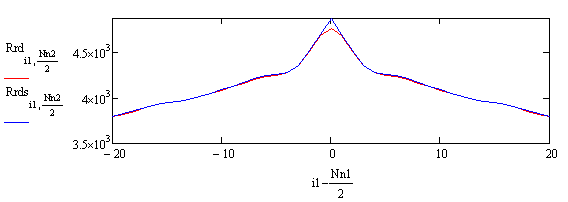
Рис.2. Графики разрезов автокорреляционных
функций изображения рис.1А (красная линия)
и изображения рис.1А с добавленным
нормальным шумом (синяя линия).
Рис.2 иллюстрирует тот факт,
что автокорреляционные функции изображений с добавленным некоррелированным
шумом и без него отличаются только в нуле [4 – 6]. Для того, чтобы оценить
значение ![]() , воспользуемся параболической интерполяцией:
, воспользуемся параболической интерполяцией:
![]() . (3)
. (3)
К сожалению, рекомендуемая [4 – 6] линейная экстраполяция дает удовлетворительные результаты только при больших уровнях шума.
На рис.3 представлены
графики зависимости ошибки в оценке дисперсии ![]() шума
от среднеквадратичного значения шума
шума
от среднеквадратичного значения шума ![]() при условии
параболической интерполяции (3).
при условии
параболической интерполяции (3).
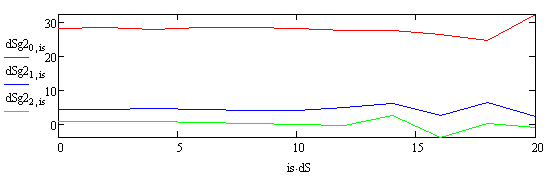
Рис.3. Графики зависимости ошибки в
оценке дисперсии ![]() шума от среднеквадратичного
значения шума
шума от среднеквадратичного
значения шума ![]() при условии параболической
интерполяции при различных значениях S0 искажающей аппаратной функции дефокусировки [7]. S0=0 – красная линия, S0=2 – синяя линия и S0=4 – зеленая линия.
при условии параболической
интерполяции при различных значениях S0 искажающей аппаратной функции дефокусировки [7]. S0=0 – красная линия, S0=2 – синяя линия и S0=4 – зеленая линия.
При увеличении ![]() графики на рис.3 становятся из прямых линий
все более изломанными. Это проявление влияния недостаточной статистики при
больших значениях
графики на рис.3 становятся из прямых линий
все более изломанными. Это проявление влияния недостаточной статистики при
больших значениях ![]() . Величина ошибки при прочих
равных условиях уменьшается с ростом S0. На рис.4 представлены графики зависимости ошибки в оценке дисперсии
. Величина ошибки при прочих
равных условиях уменьшается с ростом S0. На рис.4 представлены графики зависимости ошибки в оценке дисперсии ![]() от S0 для аппаратных функций Гаусса [8] и дефокусировки [7].
от S0 для аппаратных функций Гаусса [8] и дефокусировки [7].
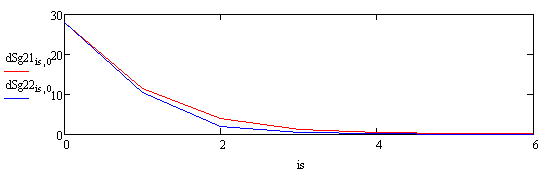
Рис.4. Графики зависимости ошибки в
оценке дисперсии ![]() шума от S0
шума от S0
искажающей аппаратной функции
Гаусса – синяя линия и дефокусировки – красная линия.
Уменьшение ошибки в оценке
дисперсии ![]() при увеличении значения S0, которое
определяет степень «размытости» изображения, объясняется тем, что «пик»
автокорреляционной функции изображения в нуле становится менее острым и более
сглаженным. Это уменьшает ошибку при интерполяции. С другой стороны, в силу
того, что обычно величина шума существенно меньше яркости изображения, ошибки в
определении дисперсии
при увеличении значения S0, которое
определяет степень «размытости» изображения, объясняется тем, что «пик»
автокорреляционной функции изображения в нуле становится менее острым и более
сглаженным. Это уменьшает ошибку при интерполяции. С другой стороны, в силу
того, что обычно величина шума существенно меньше яркости изображения, ошибки в
определении дисперсии ![]() могут быть значительны.
могут быть значительны.
Предположим, что дисперсию ![]() мы определили без ошибки, шум
некоррелированный и, следовательно, имеет место равномерный усредненный спектр.
В этом случае можно, воспользовавшись фильтрацией по Винеру [1-6], восстановить
изображение в том случае, если нам известен амплитудный спектр изображения без
шума. На первый взгляд кажется, что знание
мы определили без ошибки, шум
некоррелированный и, следовательно, имеет место равномерный усредненный спектр.
В этом случае можно, воспользовавшись фильтрацией по Винеру [1-6], восстановить
изображение в том случае, если нам известен амплитудный спектр изображения без
шума. На первый взгляд кажется, что знание ![]() позволяет
оценить искаженное изображение без шума. На самом деле это не так, потому что
спектр зашумленного искаженного изображения, как правило, содержит области,
почти целиком заполненные шумом. Поэтому оценить уровень сигнала, зная только
уровень шума, в этих областях нельзя.
позволяет
оценить искаженное изображение без шума. На самом деле это не так, потому что
спектр зашумленного искаженного изображения, как правило, содержит области,
почти целиком заполненные шумом. Поэтому оценить уровень сигнала, зная только
уровень шума, в этих областях нельзя.
Решить эту задачу можно, если в качестве оценки амплитудного спектра неискаженного сигнала использовать универсальный опорный спектр (УОС) [8, 13].
Запишем фильтрацию с помощью фильтра Винера в виде [1, 2]:
![]() , (4)
, (4)
где ![]() и
и ![]() - спектры восстановленного и искаженного
зашумленного изображений соответственно;
- спектры восстановленного и искаженного
зашумленного изображений соответственно; ![]() -
спектр аппаратной функции (АФ);
-
спектр аппаратной функции (АФ); ![]() и
и ![]() - спектральные частоты;
- спектральные частоты; ![]() и
и ![]() -
спектральные мощности соответственно исходного неискаженного изображения и
шума;
-
спектральные мощности соответственно исходного неискаженного изображения и
шума; ![]() - фильтр Винера (ФВ), рассчитанный по
формуле [1, 2]:
- фильтр Винера (ФВ), рассчитанный по
формуле [1, 2]:
Если ![]() можно
оценить с помощью
можно
оценить с помощью ![]() , то в качестве оценки
, то в качестве оценки ![]() можно использовать квадрат модуля УОС. На
рис.5 представлены искаженное зашумленное и восстановленное с помощью (4,5)
изображения.
можно использовать квадрат модуля УОС. На
рис.5 представлены искаженное зашумленное и восстановленное с помощью (4,5)
изображения.
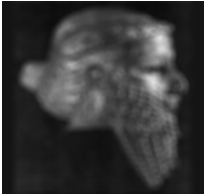
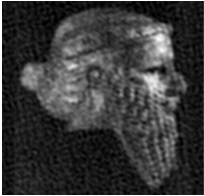

А Б В
Рис.5. Искаженное и зашумленное
нормальным шумом с ![]() =10 изображение – А. АФ
соответствует дефокусировке с S0=6. При
восстановлении считается, что параметры шума известны. Восстановление
изображений производится с помощью ФВ. Восстановление при известном исходном
изображении – Б. Восстановление с помощью УОС – В.
=10 изображение – А. АФ
соответствует дефокусировке с S0=6. При
восстановлении считается, что параметры шума известны. Восстановление
изображений производится с помощью ФВ. Восстановление при известном исходном
изображении – Б. Восстановление с помощью УОС – В.
Рис.5Б и рис.5В мало
отличаются, что подтверждает возможность замены ![]() на
УОС.
на
УОС.
Вывод: восстановление изображения с
помощью ФВ требует знания спектральных мощностей исходного неискаженного
изображения и шума. В случае некоррелированного шума его характеристиками
являются дисперсия и плотность распределения. Определение дисперсии возможно с
помощью известной функции автокорреляции изображения [4 – 6]. Использование УОС
в качестве ![]() делает возможным восстановление
изображения с помощью ФВ.
делает возможным восстановление
изображения с помощью ФВ.
2. Коррелированный шум
Для того чтобы рассмотреть способы восстановления изображения с помощью ФВ, сформируем такой шум, который имеет заданную спектральную мощность.
Сформируем нормальный некоррелированный шум. Его спектр модулируем по Гауссу:
![]() , (6)
, (6)
где ![]() и
и ![]() - спектры некоррелированного нормального
шума и модулированного шума соответственно;
- спектры некоррелированного нормального
шума и модулированного шума соответственно; ![]() -
константа, задающая скорость уменьшения амплитуды спектра модулированного шума
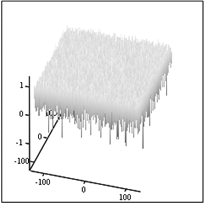
с возрастанием частоты. На рис.6 представлены спектры нормального,
модулированного шума и сам сформированный шум.
-
константа, задающая скорость уменьшения амплитуды спектра модулированного шума
с возрастанием частоты. На рис.6 представлены спектры нормального,
модулированного шума и сам сформированный шум.
А Б В
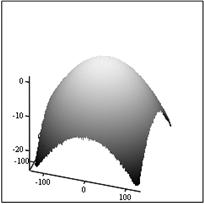
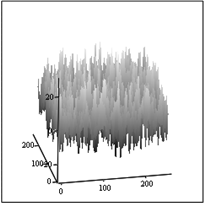
Рис.6. Спектр нормального шума – А,
спектр модулированного шума – Б. Оба спектра по оси z в логарифмическом масштабе.
Полученный модулированный шум –
В.
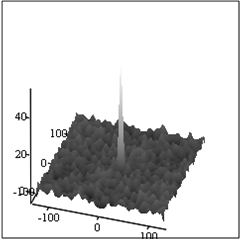
Понятно, что полученный модулированный шум, спектр которого соответствует (6), является коррелированным с функцией автокорреляции, график которой представлен на рис.7.
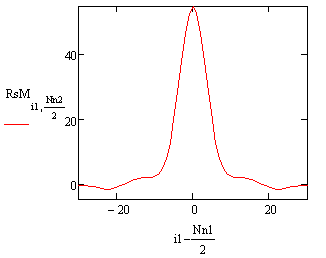
А Б
Рис.7. Функция автокорреляции шума – А и график ее разреза – Б.
Рассмотрим автокорреляционные функции изображений (S0=6) без шума и с шумом. На рис.8 представлены графики разрезов этих функций.
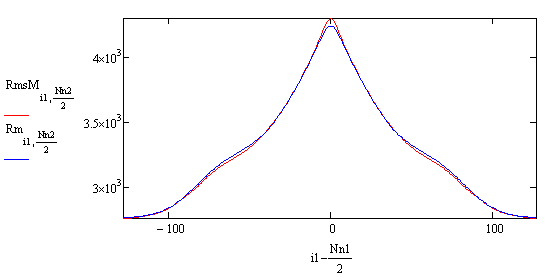
А
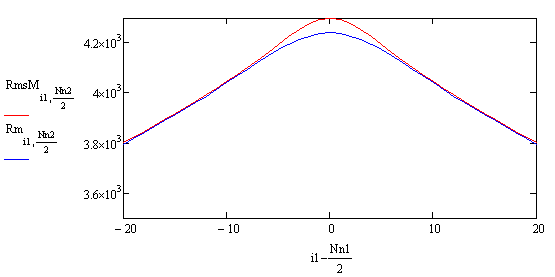
Б
Рис.8. Графики разрезов автокорреляционных функций изображений с коррелированным шумом – красная линия и без шума – синяя линия. Полный и частичный графики разрезов соответствуют рисункам А и Б.
Графики на рис.8
иллюстрируют факт, что в случае коррелированного шума способ [4 – 6] определения
![]() и функции автокорреляции шума
малоперспективен. Более того, знание
и функции автокорреляции шума
малоперспективен. Более того, знание ![]() не позволяет
использовать ФВ, поскольку остается неизвестным спектр мощности шума
не позволяет
использовать ФВ, поскольку остается неизвестным спектр мощности шума ![]() . Возможное решение этой проблемы
позволяет восстанавливать искаженное зашумленное изображение с помощью ФВ в
отсутствие информации о шуме и неискаженном изображении.
. Возможное решение этой проблемы
позволяет восстанавливать искаженное зашумленное изображение с помощью ФВ в
отсутствие информации о шуме и неискаженном изображении.
Для этого будем считать, что:
1. УОС позволяет достаточно хорошо оценивать спектр мощности неискаженного изображения.
2. В качестве оценки спектра мощности
шума ![]() можно использовать
можно использовать ![]() , где
, где ![]() обозначает
УОС.
обозначает
УОС.
При этих условиях (5) будет иметь вид:
Искаженное и зашумленное
коррелированным шумом рис.6В изображение представлено на рис.9А.
Восстановленные с помощью ФВ изображения представлены на рис.9Б и рис.9В,
причем предполагалось, что спектр мощности шума ![]() известен,
а в качестве спектра мощности неискаженного сигнала при получении рис.9В
используется УОС. Сравнение рис.9Б и рис.9В позволяет сделать вывод о хорошей
оценке с помощью УОС спектра мощности неискаженного сигнала.
известен,
а в качестве спектра мощности неискаженного сигнала при получении рис.9В
используется УОС. Сравнение рис.9Б и рис.9В позволяет сделать вывод о хорошей
оценке с помощью УОС спектра мощности неискаженного сигнала.


А Б В
Рис.9. Искаженное и зашумленное
коррелированным шумом рис.6В изображение – А.
Восстановленные изображения с
помощью ФВ – Б и В.
Восстановление производилось при условии известных спектров
![]() и
и ![]() - Б.
- Б.
В
случае рис.9В известен только ![]() , а в качестве
, а в качестве ![]() используется УОС.
используется УОС.
Однако на практике спектр мощности
коррелированного шума часто неизвестен. Поэтому обычно его заменяют выбранным,
исходя из визуальных предпочтений, постоянным значением. На рис.10 представлены
восстановленные с помощью ФВ (5) и (7) изображения, причем рис.10А
соответствует (5), где в качестве ![]() используется УОС, а
используется УОС, а ![]() заменено выбранной константой. На рис.10Б
представлено изображение, полученное с помощью (7).
заменено выбранной константой. На рис.10Б
представлено изображение, полученное с помощью (7).

А Б
Рис.10. Восстановленные изображения рис.9А
с помощью ФВ (5), где в качестве ![]() используется УОС,
используется УОС,
а
неизвестный спектр шума при восстановлении заменен на подобранную константу – А;
результаты вычислений на основе (7) – Б.
Сравнение результатов
вычислений ФВ (5) и (7) на рис.10 позволяет сделать вывод об относительной
эффективности определения спектра сигнала ![]() и
спектра шума
и
спектра шума ![]() с помощью УОС. Другим вариантом учета
влияния неизвестного шума на восстановление изображения является реконструкция
амплитудного спектра неискаженного изображения по инверсно отфильтрованному
спектру [9]. Особенно целесообразно применить такой подход к случаю
локально-спектральных помех (ЛСП). В данной работе мы не будем рассматривать
реализацию такого решения с помощью ФВ.
с помощью УОС. Другим вариантом учета
влияния неизвестного шума на восстановление изображения является реконструкция
амплитудного спектра неискаженного изображения по инверсно отфильтрованному
спектру [9]. Особенно целесообразно применить такой подход к случаю
локально-спектральных помех (ЛСП). В данной работе мы не будем рассматривать
реализацию такого решения с помощью ФВ.
3. Локально-спектральные помехи
Восстановление изображений при наличии локально-спектральных помех (ЛСП) возможно различными методами [1 – 3, 5, 6, 9 – 12]. Часто рассматривается лишь случай фильтрации таких помех от неискаженного АФ изображения [1 – 3, 5, 6, 10, 11]. Предполагается, что перед такой фильтрацией обязательно нужно изучить свойства помехи. Сама фильтрация производится с помощью маски, режекторного фильтра или ФВ после установления координат помехи на спектре изображения.
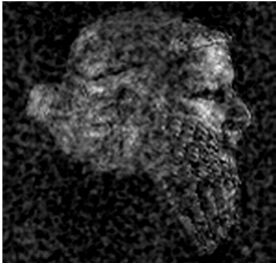
Рассмотрим изображение, искаженное АФ с S0=6 и зашумленное ЛСП в виде полос – рис.11.
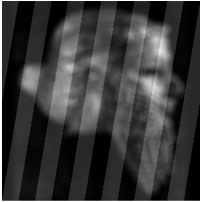
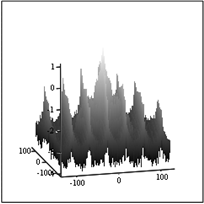
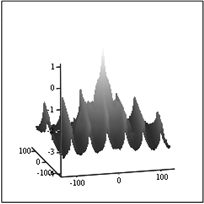
А Б В
Рис.11. Изображение искаженное АФ с S0=10 и ЛСП «полосы» - А; его спектр – Б и усредненный спектр по спрайту 5х5 пикселов – В.
Спектры на рис.11 показывают
ЛСП «полосы» в виде изрезанных бугров, причем усреднение по спрайту 5х5 не
вызвало значительного уменьшения амплитуды этих бугров. В работах [5,
6]
говорится о том, что «Возможность обнаружения основывается на предположении о
том, что последовательность ![]() в среднем является
«гладкой», т. е. ее элементы не должны значительно отличаться от ближайших к
ним. Поэтому локализованные выбросы, сильно отличающиеся от своего окружения,
могут быть квалифицированы как компоненты, искаженные помехой.». Таким образом,
поиск локально-спектральной помехи сводится к поиску выбросов на фоне
усредненного спектра. В случае, когда ЛСП представляет собой одиночные выбросы,
это так. На рис.11 представлен случай ЛСП в виде «бугров». В таком случае
использование алгоритма [5, 6] становится затрудненным в силу того, что усредненный
спектр рис.11В (на фоне которого ищется ЛСП) имеет такие же «бугры» как и
спектр на рис.11Б.
в среднем является
«гладкой», т. е. ее элементы не должны значительно отличаться от ближайших к
ним. Поэтому локализованные выбросы, сильно отличающиеся от своего окружения,
могут быть квалифицированы как компоненты, искаженные помехой.». Таким образом,
поиск локально-спектральной помехи сводится к поиску выбросов на фоне
усредненного спектра. В случае, когда ЛСП представляет собой одиночные выбросы,
это так. На рис.11 представлен случай ЛСП в виде «бугров». В таком случае
использование алгоритма [5, 6] становится затрудненным в силу того, что усредненный
спектр рис.11В (на фоне которого ищется ЛСП) имеет такие же «бугры» как и
спектр на рис.11Б.
Другим вариантом фильтрации ЛСП может быть секвентный анализ [10, 11]. В рамках этого метода помехи классифицируются, изучаются их характеристики на основе моделирования помехи и затем производится фильтрация на основе сконструированного фильтра.
На наш взгляд в большинстве случаев такие способы фильтрации излишне усложнены. После применения (7) к спектру на рис.11Б можно получить результат, представленный на рис.12. На этом рисунке видно, что с помощью (7) удалось полностью отфильтровать помеху.

А Б
Рис.12. Восстановленное с помощью (7) изображение рис.11А – А и его спектр – Б.
Использование ФВ для восстановления предполагает наличие искажений АФ. Если такие искажения отсутствуют, то можно воспользоваться для фильтрации от помех методом перенормировки с ограничением [9].
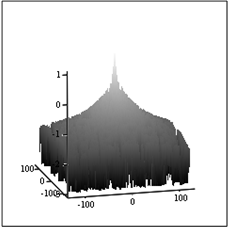
В силу того, что в ряде работ авторы [4 – 6] предлагают воспользоваться для фильтрации помех свойством «гладкости» спектра изображения. Для проверки такого способа фильтрации сформируем спектр изображения, искаженного АФ с S0=6 с добавлением помехи нормального шума расположенного на спектре в виде широкого бугра – рис.13.
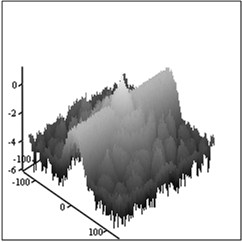
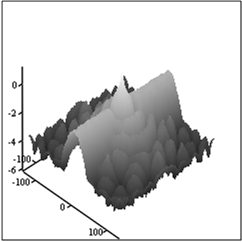
А Б
Рис.13. Спектры искаженного
изображения с локально-спектральной помехой.
Спектр изображения – А и
усредненный по спрайту 5х5 пикселов – Б.
Сравнение рис.13А и рис.13Б показывает, что усреднение повлияло на вид спектра слабо. Следовательно, использовать свойство «гладкости» для идентификации помехи в данном случае неэффективно. На рис.14 представлены изображение с помехой на рис.13 и изображения, восстановленные ФВ.
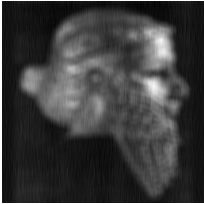


А Б В
Рис.14. Изображение с помехой – А,
изображения, восстановленные ФВ – Б и В.
Восстановленное изображение с заменой
спектра мощности шума на подобранную константу – Б, с помощью (7) – В.
Анализ результатов восстановления изображения с ЛСП с помощью ФВ (5) и (7) позволяют сделать вывод о достаточно эффективной фильтрации изображения ФВ (7).
Выводы
1. Дисперсия некоррелированного шума ![]() может быть оценена с помощью способа,
описанного в ряде работ [4 – 6]. Ошибка такой оценки зависит от искажающей
изображение АФ. Эта ошибка уменьшается с величиной искажения S0. Использование УОС при известной
может быть оценена с помощью способа,
описанного в ряде работ [4 – 6]. Ошибка такой оценки зависит от искажающей
изображение АФ. Эта ошибка уменьшается с величиной искажения S0. Использование УОС при известной ![]() позволяет восстановить искаженное АФ
зашумленное изображение.
позволяет восстановить искаженное АФ
зашумленное изображение.
2. При коррелированном шуме для восстановления изображения необходимо знать спектр функции автокорреляции шума. Способ ее определения [4 – 6] не позволяет это сделать корректно. Использование для восстановления в этом случае ФВ (7) не требует оценки функции автокорреляции шума.
3. Рассмотренные случаи локально-спектральных помех подтверждают достаточно высокую эффективность применения и простоту ФВ (7) по сравнению с альтернативными способами (использование «гладкости» спектра [5 – 6] и секвентного анализа [10 – 11]).
4. Модификация ФВ с использованием УОС позволяет восстанавливать изображение с неизвестными аддитивными шумами и помехами.
Литература
1. Р. Гонсалес, Р. Вудс. Цифровая обработка изображений. М. «Техносфера», 2005, 1071 стр.
2. Pratt W.K. Digital Image Processing. – John Wiley and Sons, Inc., USA, 1978.
3. Бейтс Р. Мак-Доннел М. Восстановление и реконструкция изображений. /Пер. с англ.к. ф-м н. Б.С. Кругликова и С.Л. Ярославского под редакцией д. ф-м н. Л.П. Ярославского. М.: «Мир», 1989, 487с.
4. Миркин Л. И., Ярославский Л. П. Способ измерения зашумленности изображений. — Вопросы кибернетики: Иконика, цифровая обработка и фильтрация изображений, 1978, вып. 38. с. 97.
5. Ярославский Л. П. Введение в цифровую обработку изображений. – М.: Сов. радио, 1979. – 312 с.
6. Ярославский Л. П. Цифровая обработка сигналов в оптике и голографии . Введение в цифровую оптику. – М.: Радио и связь, 1987. – 296 с.
7. А. Ю. Зражевский, В. А. Коротков, К. В. Коротков, Типичные проблемы восстановления изображений: дефокусировка и смазанное изображение. Результаты применения метода опорного изображения. Журнал радиоэлектроники [электронный журнал]. 2014. №4. URL: http://jre.cplire.ru/jre/apr14/11/text.html
8. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин «Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 3. Универсальный опорный спектр. // Журнал радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/3/text.html
9. А. В. Кокошкин, В. А. Коротков, К. В. Коротков, Е. П. Новичихин , Использование метода перенормировки с ограничением для восстановления искаженных изображений при наличии помех и шума с неизвестными параметрами. Журнал радиоэлектроники [электронный журнал]. 2015. №7. URL: http://jre.cplire.ru/jre/jul15/4/text.html
10. В. А. Саблина «Разработка и исследование алгоритмов восстановления изображений методами секвентного анализа». Автореферат диссертации на соискание ученой степени кандидата технических наук. Рязань, 2009г.
11. Б. В. Костров «Теория и методология применения секвентного анализа для обработки аэрокосмических изображений». Автореферат диссертации на соискание ученой степени доктора технических наук, Рязань, 2012г.
12. А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков «Влияние спектрально-локальных помех на восстановление изображения методом опорного изображения». // Журнал радиоэлектроники [электронный журнал]. 2014. №1. URL: http://jre.cplire.ru/jre/jan14/9/text.html
13. Зражевский А. Ю., Кокошкин А. В., Коротков В. А., Коротков К. В., Новичихин Е.П. «Универсальный опорный спектр и его использование для нахождения аппаратной функции искажения и восстановления изображений». Доклады VIII Всероссийской научно-технической конференции "Радиолокация и радиосвязь", 24-26 ноября 2014г., Издание JRE – ИРЭ им. В.А.Котельникова РАН, Москва 2014г., с.191.