• Исследования синхронизации и хаоса в ансамблях нелинейных осцилляторов

  Руководитель направления Кузнецов Александр Петрович вед. науч. сотр., д.ф.-м.н., профессор эл. почта: kuzalexp@yandex.ru

  
  

  Задачи о динамике ансамблей нелинейных осцилляторов продолжают привлекать внимание, как с фундаментальной точки зрения, так и с точки зрения приложений в различных областях естествознания (радиофизика, оптика, биология, химия и др.). Заделом для данного направления в лаборатории явились задачи о динамике связанных осцилляторов ван дер Поля, фазовых осцилляторов, а также хаотических осцилляторов Ресслера. Обсуждались такие вопросы, как различные типы синхронизации в таких системах, их бифуркационные механизмы, реализация сценария рождения турбулентности Ландау-Хопфа, рождение квазипериодичности разной размерности при взаимодействии хаотических осцилляторов и др. Далее рассмотрены такие задачи, как синхронизация систем с квазипериодической динамикой. Исследовалась вынужденная синхронизация генераторов квазипериодических колебаний, динамика двух связанных генераторов, возбуждение двух генераторов внешним сигналом, динамика трех генераторов. Выявлены различные типы синхронизации в таких системах. На базе систем с непрерывным временем предложено семейство дискретных моделей. В рамках этих задач обсуждается фундаментальная проблема бифуркаций инвариантных торов разной размерности, являющихся образами квазипериодических колебаний с разным числом несоизмеримых частот. Исследовались сценарии рождения хаоса и гиперхаоса при разрушении многочастотных торов в предложенной модели многоконтурного генератора. В качестве одного из примеров исследуется также система неидентичных контактов Джозефсона. Результаты 2023 года относятся к случаю взаимодействия подсистем с квазипериодической и хаотической динамикой, позволяющего исследовать эволюцию режимов и их бифуркации при увеличении силы связи.

  

  Карта ляпуновских показателей двух связанных генераторов квазипериодических колебаний, P – периодический режим, T₂ - двухчастотный тор, T₃ - трехчастотный тор, T₄ - четырехчастотный тор, C – хаос. Новые типы режимов синхронизации: SC – область синхронной квазипериодичности, BS – область широкополосной синхронизации, BQ – область широкополосной двухчастотной квазипериодичности.

  

  Графики ляпуновских показателей связанных систем с квазипериодической и хаотической динамикой в зависимости от величины связи, иллюстрирующие рождение из хаоса трехчастотных торов 3Т и двухчастотных торов 2Т. QH – квазипериодическая бифуркация Хопфа инвариантного тора, DT - бифуркации удвоения трехчастотного тора.

• Численные методы анализа нелинейных динамических эффектов

  Руководитель направления Купцов Павел Владимирович г.н.с., д.ф.-м.н, профессор эл. почта: kupav@mail.ru

  
  

  Сложная динамика нелинейных системы систем в большинстве случаев не может быть исследована аналитическими методами. Поэтому в лаборатории большое значение придаётся развитию численных подходов. В рамках этого направления прорабатываются задачи, связанные с развитием методов ляпуновского анализа, а также задачи о применении методов машинного обучения и науки о данных для анализа нелинейной динамики.
  Понятие ляпуновского анализа восходит к идеям теории устойчивости движения А. М. Ляпунова, которые были распространены на случай хаотической динамики благодаря мультипликативной эргодической теореме В. И. Оселедца. В основе ляпуновского анализа, который в большинстве случаев может быть выполнен только численно, лежит исследование векторов касательных возмущений к траекториям динамической системы. Центральная роль принадлежит так называемым ляпуновским показателям, характеризующим экспоненциальный рост или убыль объёмов, построенных на этих векторах. По значениям показателей можно судить о характере динамики системы. Более детальное описание динамики можно получить, вычисляя ковариантные ляпуновские вектора, а также различные статистические характеристики конечновременных приращений векторов.
  Развитие методов ляпуновского анализа в лаборатории связано с исследованием характера хаотической динамики, в частности – с выявлением гиперболического и псевдогиперболического хаоса. Разработан эффективный численный метод проверки гиперболичности, основанный на вычислении углов между ковариантными ляпуновскими векторами. Предложены методы анализа хаоса на основе исследования распределений конечновременных показателей на асимптотически больших и малых временах. Сформулирована концепция мгновенных показателей Ляпунова как предельный случай конечновременных приращений при стремлении интервала времени к нулю.
  Машинное обучение и наука о данных накопили много идей анализа сложных систем на основе наблюдаемых величин. При исследовании нелинейной динамики также часто доступны только наблюдаемые – либо полученные как численные решения уравнений эволюции, либо записанные в эксперименте. Поэтому в лаборатории ведутся исследования на стыке нелинейной динамики и машинного обучения. С использованием нейронной сети-автокодировщика найдено низкоразмерное инерциальное многообразие, содержащее хаотический аттрактор распределённой системы. Разработано нейросетевое отображение, которое можно обучить моделировать динамику широкого круга систем.
  

  

  

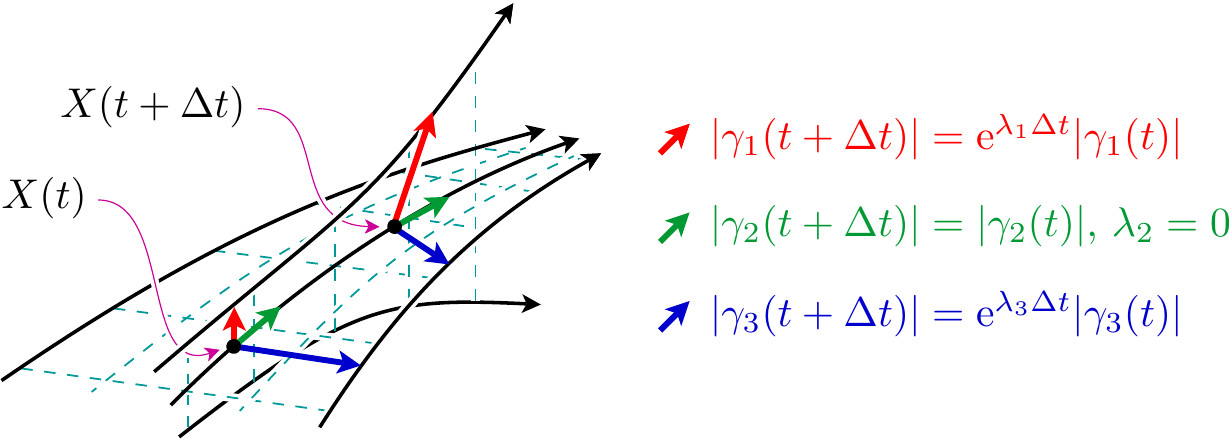
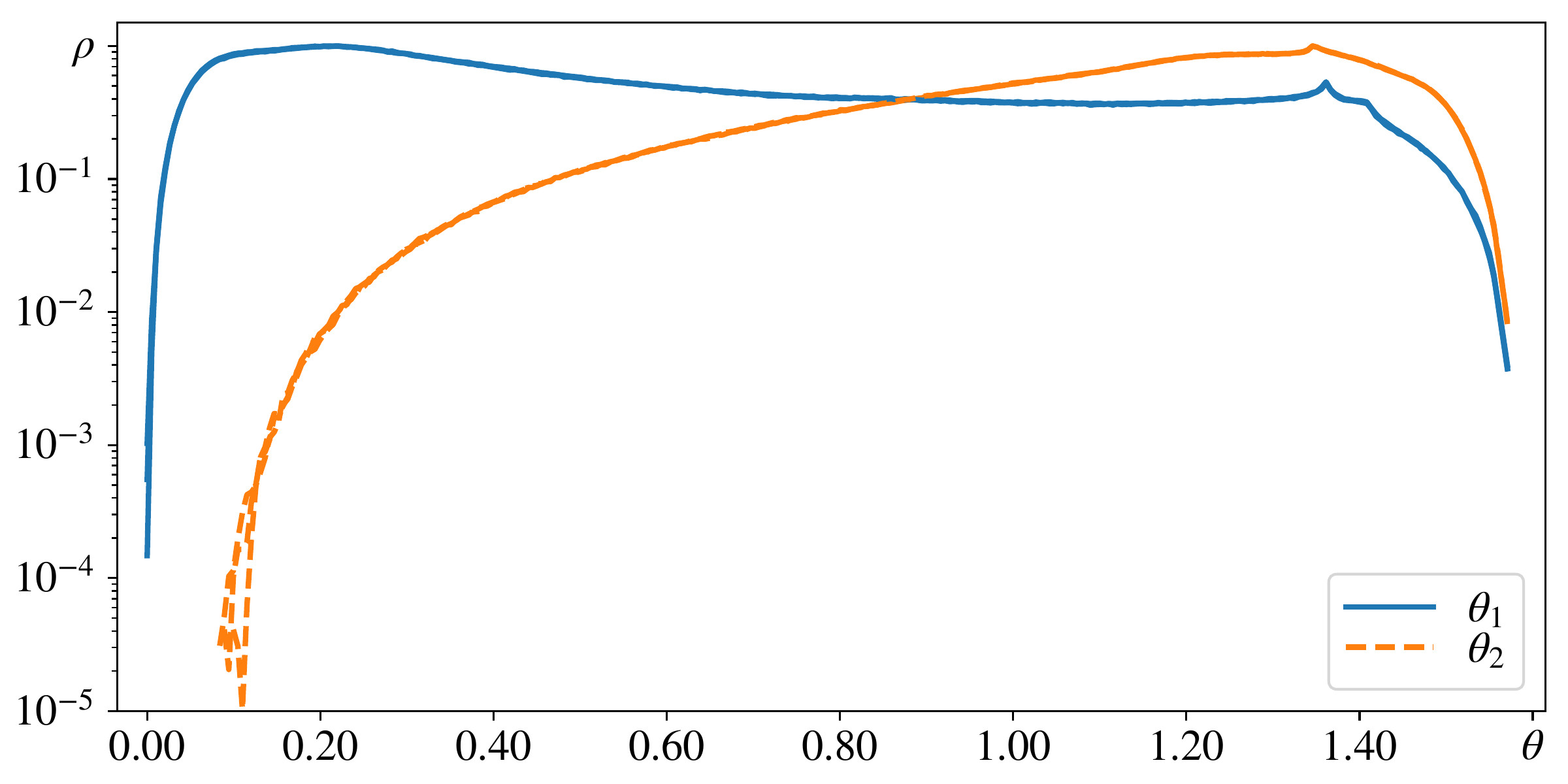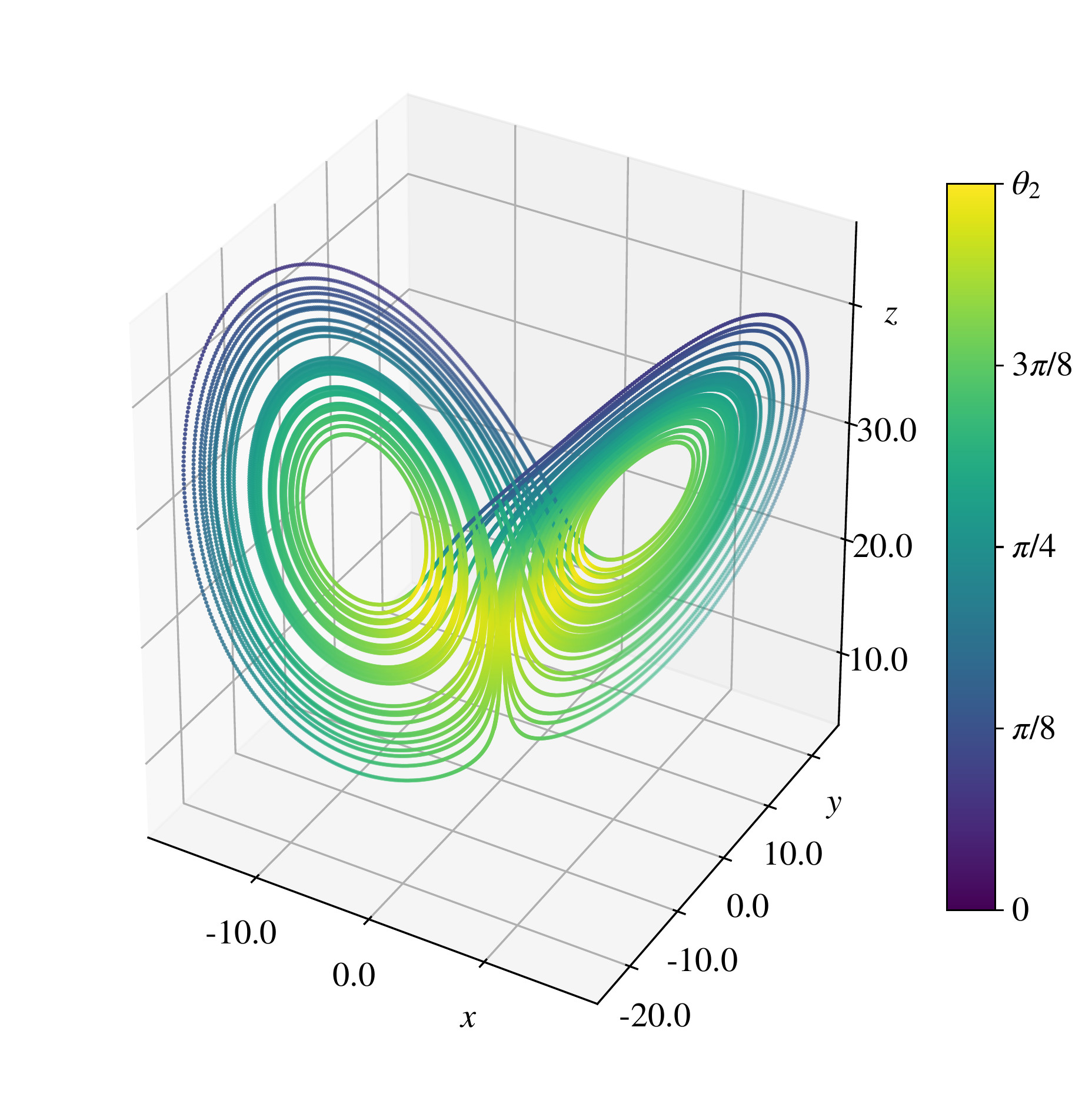
  На рисунке сверху – схематическое изображение сближающихся и разбегающихся траекторий (чёрные кривые), соответствующие ковариантные ляпуновские вектора (красный зелёный и синий) и выражения для показателей Ляпунова, показывающие как нарастают и убывают ковариантные вектора. На рисунках ниже – распределения углов между растягивающимся, нейтральным и сжимающимся многообразиями на аттракторе Лоренца и сам аттрактор Лоренца, раскрашенный в соответствии со значениями углов.

  

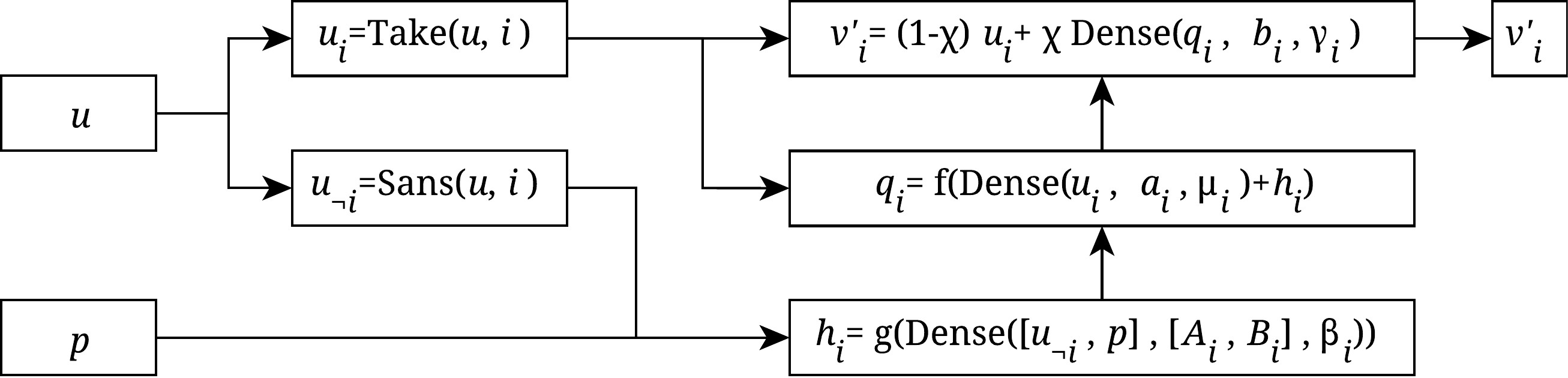
  Структурная схема нейросетевого отображения, которое может быть обучено для моделирования динамики широкого круга динамических систем.

• Анализ аттракторов со сложной структурой

  Руководитель направления Сатаев Игорь Рустамович в.н.с., к.ф.-м.н эл. почта: sataevir@gmail.com

  
  

  В рамках этого направления рассматриваются следующие вопросы.
  Сценарии перехода к хаосу и сложная динамика на границе “порядок-хаос”: ренормгрупповой анализ, критическое поведение.
  Сценарии возникновения гиперхаотических аттракторов: каскады бифуркаций рождения тора резонансных циклов и последующий каскад возникновения гиперхаотических спиральных аттракторов Шильникова.
  Хаотические аттракторы с дополнительными нулевыми показателями Ляпунова: аттракторы, возникающие после каскада удвоения тора, динамика систем с периодическим воздействием.
  Особенности хаотического аттрактора в квазипериодически возбуждаемых нелинейных осцилляторах.
  Гиперболические хаотические аттракторы: принципы конструирования систем с гиперболическим аттрактором Смейла-Вильямса, сценарии возникновения гиперболических аттракторов Смейла-Вильямса и Плыкина.
  

  

  

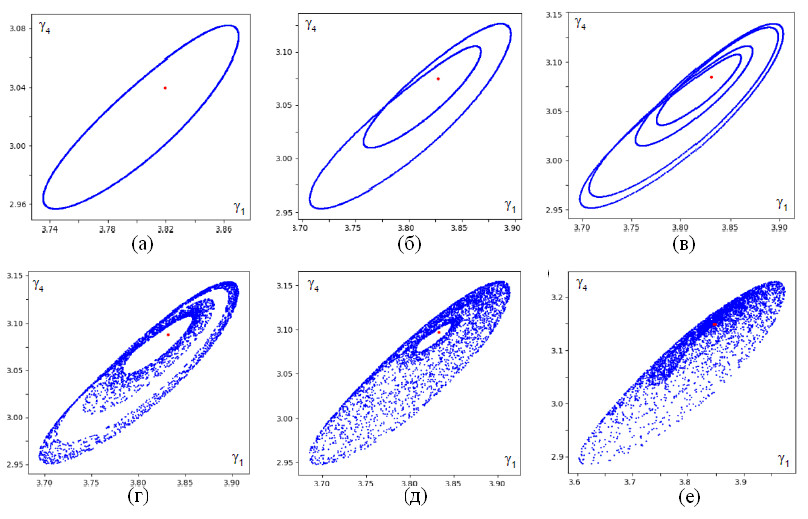
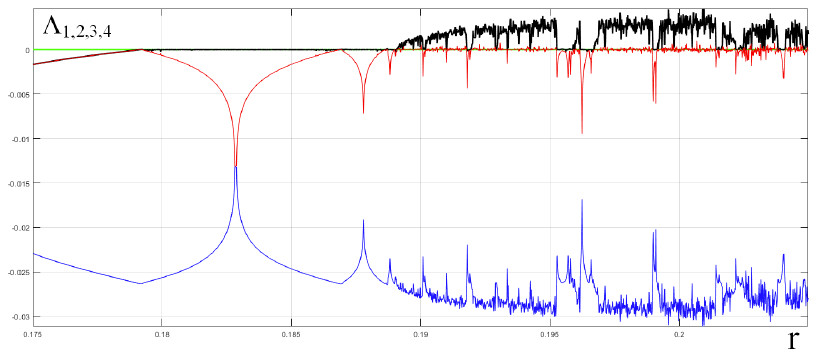
  Фазовые портреты аттрактора в сечении Пуанкаре и графики ляпуновских показателей, иллюстрирующие сценарий рождения дискретного аттрактора Шильникова

  

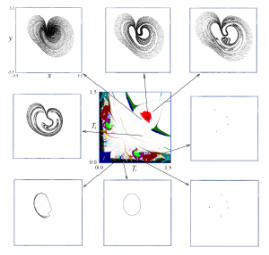
  В центре показана карта режимов системы с аттрактором Плыкина. Черный цвет соответствует квазипериодическим режимам, белый - хаотическим, а остальные цвета обозначают периодические режимы. Область существования гиперболического хаотического аттрактор показана красным цветом. По периферии представлены характерные фазовые портреты.

• Синхронизация связанных квазипериодических генераторов

  Изучена синхронизация, ее бифуркационные механизмы и хаотическая динамика двух и трех связанных, а также возбуждаемых генераторов, способных демонстрировать квазипериодические автономные колебания. Обнаружены режимы синхронной квазипериодичности, широкополосной синхронизации и широкополосной квазипериодичности. Рассмотрены ситуации разных типов настройки индивидуальных генераторов (периодические колебания, квазипериодические колебания). Проведен детальный численный бифуркационный анализ состояния равновесия и предельных циклов, формирующих сложную картину динамических режимов. Рассмотрены бифуркации инвариантных торов. Обсуждается аналогия и отличия от случая связанных осцилляторов ван дер Поля. Результаты могут иметь фундаментальное значение для теории синхронизации квазипериодических колебаний, а также теории бифуркаций инвариантных торов.

  

  Однопараметрическая бифуркационная диаграмма и бифуркационные линии на плоскости параметров для трех связанных квазипериодических генераторов.

  Публикации:
  
  • A.P. Kuznetsov, S.P. Kuznetsov, N.A. Shchegoleva, N.V. Stankevich. Dynamics of coupled generators of quasiperiodic oscillations: Different types of synchronization and other phenomena. Physica D, 2019, v. 398, p. 1-12
  • А.П. Кузнецов, Ю.В. Седова, Н.В. Станкевич. Два связанных квазипериодических генератора, возбуждаемых гармоническим сигналом. Журнал технической физики, 2021, вып. 11, с. 1619-1624
  • А.П. Кузнецов, Ю.В. Седова, Н.В. Станкевич. Различные режимы трех связанных генераторов, способных демонстрировать квазипериодические колебания. Письма в Журнал технической физики. 2022, вып. 24, с. 19-22
  • А.П. Кузнецов, Ю.В. Седова, Н.В. Станкевич. Динамика трех связанных квазипериодических генераторов. Дифференциальные Уравнения и Процессы Управления. 2023, №1, с. 54-77

• Хаотические аттракторы с дополнительным нулевым показателем Ляпунова

  Исследованы примеры систем, для которых для хаотического аттрактора появляется дополнительный ляпуновский показатель(квазипериодический аттрактор Эно): дискретная версия климатической модели Лоренц-84 и система пяти глобально связанных фазовых осцилляторов с бигармонической связью. Показано, что области двухчастотных торов имеют вид резонансных языков. Структура некоторых языков имеет характерные формы типа CrossRoad-Area и Spring-Area, известные ранее для периодических режимов.

  

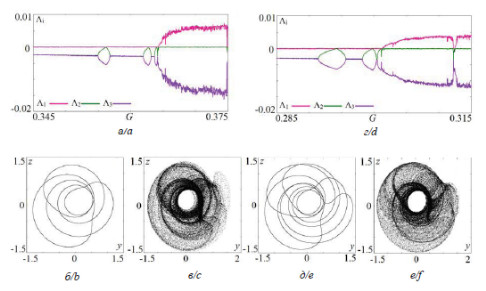
  Графики показателей Ляпунова и двумерные проекции фазовых портретов дискретного осциллятора Лоренца-84 для языков инвариантных кривых с различными числами вращения

  Публикации:
  
  • Е.С.Попова., Н.В. Станкевич, А.П. Кузнецов. Каскад бифуркаций удвоения инвариантной кривой и квазипериодический аттрактор Эно в дискретной модели Лоренца-84. Изв. Сарат. ун-та. Нов. сер. Сер. Физика. 2020, т. 20, вып. 3, с. 222-232
  • E.A. Grines., А. Kazakov, I.R. Sataev. On the origin of chaotic attractors with two zero Lyapunov exponents in a system of five biharmonically coupled phase oscillators. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2022, v. 32, №. 9, p. 093105

• Связанные системы с хаосом и квазипериодичностью

  Рассмотрено взаимодействие системы с квазипериодической автономной динамикой и хаотической системы. При малой связи реализуется хаотический режим, который может характеризоваться двумя дополнительными нулевыми показателями Ляпунова. Показано, что с ростом связи последовательно возникают трехчастотный квазипериодический режим, двухчастотный режим, периодический режим и режим гибели колебаний. В системе возможны удвоения трехчастотных торов. Дан двухпараметрический ляпуновский и бифуркационный анализ. Описан новый бифуркационный сценарий перехода в связанных системах от режима гибели колебаний к квазипериодичности. Он состоит в том, что состояние равновесия теряет устойчивость через субкритическую бифуркацию Андронова-Хопфа, сталкиваясь с седловым предельным циклом. В свою очередь этот цикл в точке седло-узловой бифуркации сливается с устойчивым. Последний испытывает бифуркацию Неймарка-Сакера, когда при уменьшении связи от него мягким образом отделяется устойчивый тор.

  

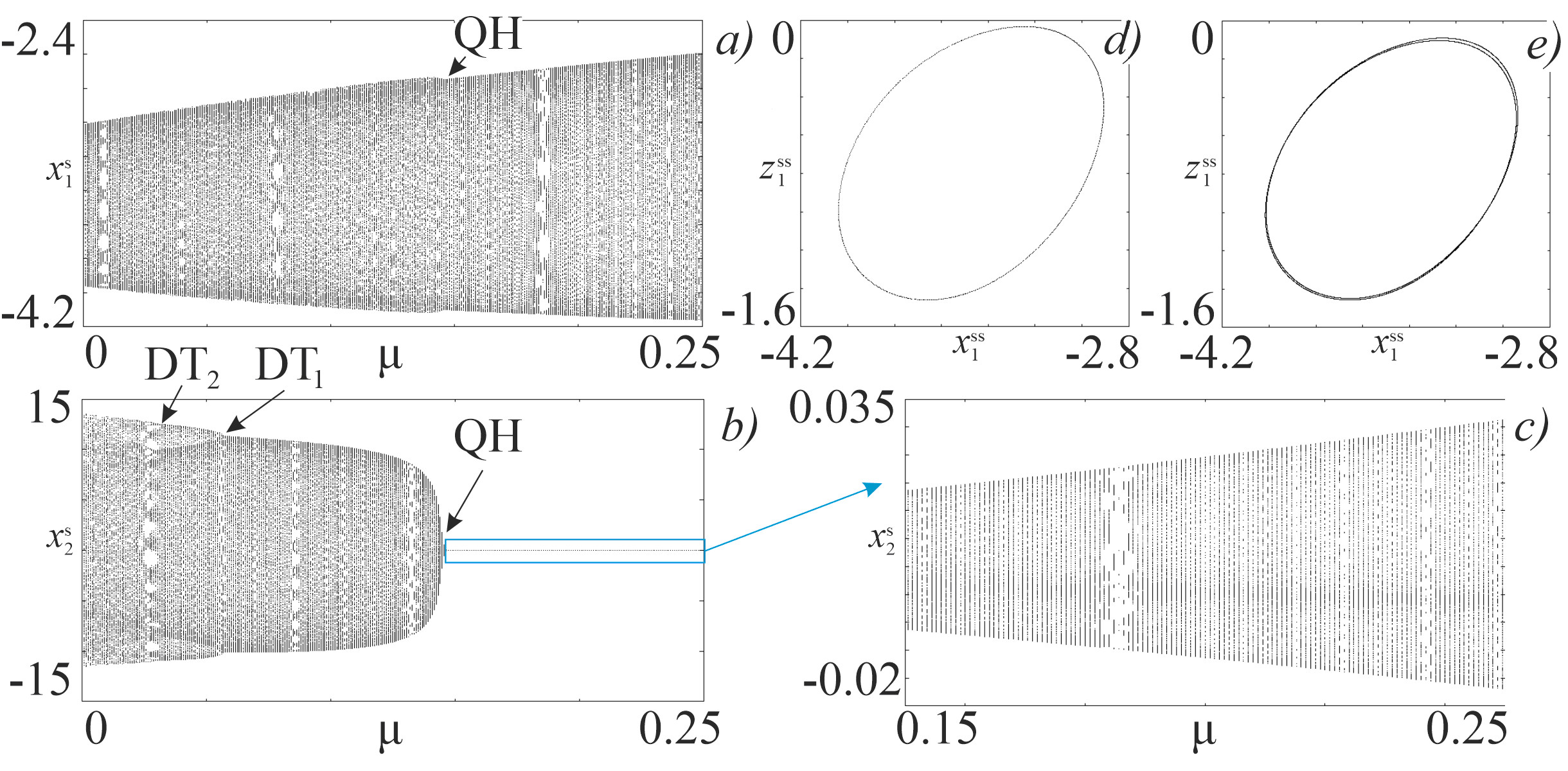
  Бифуркационное дерево в сечении Пуанкаре в проекции на переменную квазипериодической (a) и хаотической (b,c) подсистем. Отображение Пуанкаре в двойном сечении Пуанкаре (d, e). QH – квазипериодическая бифуркация Хопфа инвариантного тора, DT - бифуркации удвоения инвариантного тора.

  Публикации:
  
  • A.P. Kuznetsov. Y.V. Sedova, N.V. Stankevich. Coupled systems with quasi-periodic and chaotic dynamics. Chaos, Solitons & Fractals. 2023, v. 169, №4, p. 113278
  • А.П. Кузнецов, Ю.В. Седова. Динамика связанных квазипериодического генератора и системы Ресслера. Письма в Журнал технической физики. 2023, вып. 2, с. 17-20

• Динамика неидентичных контактов Джозефсона

  Рассматривается система трех неидентичных контактов Джозефсона, связанных через RLC цепь. Выявлены области периодических режимов, режимов двухчастотной и трехчастотной квазипериодичности, хаоса. Как правило, области двухчастотной квазипериодичности имеют вид полос разной ширины, погруженных в область трехчастотной квазипериодичности, формирующих структуру резонансной паутины Арнольда. Границами областей двухчастотной квазипериодичности являются линии седло-узловых бифуркаций инвариантных торов. С увеличением области хаоса паутина может разрушаться. Изменение типа внешней цепи, объединяющей контакты, приводит к заметному изменению вида ляпуновских карт, однако характерная область резонансной паутины сохраняется.

  

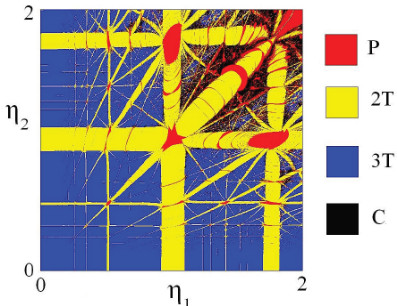
  Карта ляпуновских показателей трех контактов Джозефсона на плоскости параметров неидентичности, иллюстрирующая резонансную паутину Арнольда и ее разрушение. Показаны области периодических режимов P, двухчастотных торов 2T, трехчастотных торов 3T, хаоса С.

  Публикации:
  
  • А.П. Кузнецов, И.Р. Сатаев, Ю.В. Седова. Анализ трех неидентичных контактов Джозефсона методом карт Ляпуновских показателей. Известия Саратовского университета - Новая серия. Серия Физика. 2023, №1, с. 4-13

• Сценарий рождения гиперхаоса при разрушении многочастотных торов

  На основе ансамбля осцилляторов Ван дер Поля разработана модель многоконтурного генератора, представляющего собой ансамбль осцилляторов, связанных через общее среднее поле. Для системы с помощью спектра показателей Ляпунова проанализировано многообразие динамических режимов, которое включает периодические колебания, четыре типа многочастотных квазипериодических режимов, хаос и гиперхаос. Проведён анализ бифуркаций, сценариев развития хаотического поведения. Выявлены особенности, характерные для каждого типа хаотических аттракторов, в том числе с перспективой использования для систем связи.

  

  Карты показателей Ляпунова многоконтурного генератора

  Публикации:
  
  • N.V. Stankevich, A.P. Kuznetsov, E.P Seleznev. Chaos and hyperchaos arising from the destruction of multifrequency tori. Chaos, Solitons & Fractals . 2021, v.147, p.110998

• Исследованы эффекты синхронизации и бистабильность в системе двух связанных спин-трансферных осцилляторов

  Исследованы эффекты синхронизации и бистабильность в системе двух связанных спин-трансферных осцилляторов. Рассмотрен случай, когда осцилляторы симметричны относительно оси электрического тока, а связь осуществляет посредством магнитных полей. Обнаружен эффект бистабильности, когда сосуществуют синхронные и асинхронные колебания. Показано что в при описании осцилляторов в фазовом приближении синхронный режим соответствует неподвижной точке уравнений, а асинхронному отвечает колебательное решение. Получены аналитические оценки для границ области бистабильности в пространстве параметров. Эти оценки сопоставлены с результатами численного анализа. Результаты работы могут быть использованы для создания новой элементарной электронных и спинтронных устройств.

  

  Относительная частота появления синхронного решения при старте со случайной точки на плоскости частота-сила связи. Прерывистые линии – теоретические оценки границ области бистабильности.

  Публикации:
  
  • P.V. Kuptsov Synchronization and bistability of two uniaxial spin transfer oscillators with field coupling. Regular and Chaotic Dynamics. 2022, v. 27, No. 6, p. 697-712

• Система с гиперболическим аттрактором Смейла-Вильямса

  Предложен метод конструирования автономных моделей с гиперболическим аттрактором типа Смейла – Вильямса в сечении Пуанкаре, основанный на комплексификации двумерных потоковых систем, демонстрирующих гомоклиническую бифуркацию петли сепаратрисы седла. Фазовое пространство построенной системы состоит из двух частей, в одной из частей содержится седловое положение равновесия, в окрестности которого происходит «рассеяние» траекторий с изменением аргументов комплексных переменных в соответствии с отображением, близким к отображению Бернулли. Для этой области предложен качественный анализ, основанный на теории возмущений. На значительном расстоянии от седла аргументы комплексных переменных практически не меняются, однако рост их амплитуд ограничивается, что позволяет траекториям возвращаться в окрестность седла. В сечении Пуанкаре, установленным при достижении амплитудой одной из переменных заданного значения, возникает аттрактор, топологически схожий с соленоидом Смейла-Вильямса.

  

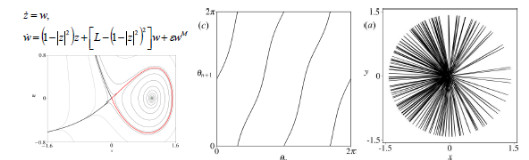
  Петля сепаратрисы седла, отображение для фаз комплексной переменной и проекция вещественной и мнимой частей переменной.

  Публикации:
  
  • S.P. Kuznetsov, V.P. Kruglov, I.R. Sataev. Smale-Williams solenoids in autonomous system with saddle equilibrium. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2021, No.1, p. 013140

• Параметрическое взаимодействие трёх волновых мод

  С использованием механического формализма Лагранжа в присутствии диссипации получена обобщённая модель, описывающая возникновение хаоса при параметрическом взаимодействии трёх мод в неравновесной среде с кубической нелинейностью. Для полученной модели, для случаев, когда параметры, имеющие смысл коэффициентов диссипации принимают положительные и отрицательные значения, была проанализирована структура пространства параметров, исследована структура аттракторов и их бассейнов притяжения, найдены основные бифуркации неподвижных точек и предельных циклов, исследована мультистабильность. Показано, что мультистабильность, обусловленная внутренней симметрией системы, проявляется независимо от знака диссипации, а мультистабильность, когда в фазовом пространстве сосуществуют аттракторы различных периодов, характерна только для случая положительной диссипации. Результаты работы могут быть использованы для анализа процессов, протекающих в неравновесных средах, и предсказания их поведения. В силу универсальности, модель отвечает системам различной физической природы, в том числе электронным, гидродинамическим, химическим.

  

  Различные сечения бассейнов притяжения устойчивых положений равновесия SP1-, SP1+. Зависимость показателей Ляпунова от параметров, примеры аттракторов.

  Публикации:
  
  • Л.В. Тюрюкина. Динамика системы Рабиновича–Фабриканта и ее обобщённой модели в случае отрицательных значений параметров, имеющих смысл коэффициентов диссипации. Известия высших учебных заведений. Прикладная нелинейная динамика. 2022, №6, с. 685-701
  • С.П.Кузнецов, Л.В. Тюрюкина. Обобщённая система Рабиновича–Фабриканта: уравнения и динамика Известия высших учебных заведений. Прикладная нелинейная динамика. 2022, №1, с. 7-29

В лаборатории выполнялось большое количество грантов РФФИ и РНФ. В 2021-2023 гг. выполняется проект РНФ "Радиофизическое моделирование сложного поведения систем различной природы и размерности в рамках универсальных подходов нелинейной динамики и теории колебаний".
В рамках Президентской программы коллектив лаборатории (совместно с лабораторией СФ-6) удостоен звания Ведущая научная школа России «Фундаментальные проблемы нелинейной динамики и их приложения».
Сотрудники лаборатории взаимодействуют с др. Анета Косеска (Институт молекулярной физиологии), Германия, проф. К. Летелье (Нормандский университет), Франция, проф. Ю. Курц (Институт изучения изменения климата), Германия, проф. Л. Чуа (Калифорнийский университет), США, проф. Н. Инаба (Университет Мейджи), Япония, а также сотрудниками Национального исследовательского университета Высшая школа экономики в Нижнем Новгороде, Саратовского национального исследовательского университета им Н.Г.Чернышевскогo, Саратовского технического университета им. Гагарина Ю.А.
На основе лаборатории была создана и функционирует базовая кафедра Динамических систем в Саратовском национальном исследовательском университете им. Н.Г.Чернышевскогo. Была разработана система взаимосвязанных учебных курсов в области нелинейной динамики, среди них «Нелинейные колебания», «Теория катастроф», «Динамические системы и бифуркации», «Приложения теории катастроф и бифуркаций», «Динамический хаос», «От порядка к хаосу», «Современные проблемы нелинейной динамики». Разработана система семинарских занятий по решению задач (большинство оригинальных) и система компьютерных практикумов по эти курсам. Были подготовлены учебники и задачники по этим направлениям, многие из которых продолжают переиздаваться. Они используются во многих вузах России и за рубежом, включая Нижегородский университет, Высшую школу экономики в Нижнем Новгороде, Московский физико-технический институт, университет Потсдама и др. Наибольшей известностью пользуются пособия А.П.Кузнецов, С.П. Кузнецов, Н.М. Рыскин. Нелинейные колебания и С.П. Кузнецов. Динамический хаос. Под руководством сотрудников лаборатории подготовлено 23 кандидатских диссертации. Среди аспирантов и студентов базовой кафедры лауреаты грантов Президента РФ для молодых ученых, стипендий Президента РФ, медали Российской академии наук, Соросовские студенты и аспиранты.

Лаборатория поддерживает сайт "Саратовская  группа Теоретической  Нелинейной  Динамики"